If the A's were distinguishable (say different colors or different sizes or
different fonts) the answer would be 6! or 720 because there are 6 letters.
However in each arrangement, say this one:
SAKALA
If the A's were colored different we could tell them apart, that is,
they would be distinguishable, like these 6:
SAKALA
SAKALA
SAKALA
SAKALA
SAKALA
SAKALA
But since they aren't colored different, those all look the same.
That is, they are indistinguishable and all look like SAKALA. So
the 720 is too many.
Now why did we know there were 6 of each arrangement that we cannot
tell the difference in? Because there are 3! or 6 ways to arrange
the three A's.
So that means that the 6! or 720 counts each arrangement 3! or 6
times too many. So we correct that by dividing 6! or 720 by 3! or 6
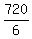= 120 distinguishable arrangements.
Edwin
