SOLUTION: What is the exact value of this expression? arcsin(sin(-3pi/5)) How do I get the answer? Thanks!

Algebra ->  Trigonometry-basics -> SOLUTION: What is the exact value of this expression? arcsin(sin(-3pi/5)) How do I get the answer? Thanks!      Log On


   

Question 808932: What is the exact value of this expression? arcsin(sin(-3pi/5))
How do I get the answer? Thanks!
Found 2 solutions by KMST, DrBeeee:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
THE SHORT ANSWER:
arcsin%28sin%28-3pi%2F5%29%29=-2pi%2F5 because
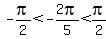
sin%28-3pi%2F5%29%29=sin%28-2pi%2F5%29 and -pi%2F2%3C-2pi%2F5%3Cpi%2F2
To find the answer you have to look for the angle that
has the same sine as -3pi%2F5
and is between -pi%2F2 and pi%2F2
sin%28-3pi%2F5%29=sin%28AOD%29=y%5BD%5D=y%5BC%5D=sin%28AOC%29=sin%28-2pi%2F5%29

THE LONG STORY:
f%28x%29=sin%28x%29 is a function and its graph looks like this:
graph%28900%2C100%2C-2%2C18%2C-1.5%2C1.5%2Csin%28x%29%2C1%2C-1%29
It is a periodic function with period 2pi ,
meaning that the same value of f%28x%29 is guaranteed to repeat at 2pi intervals.
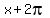The function has a maximum where f%28x%29=1 and it repeats that value 2pi later, at x%2B2pi , where f%28x%2B2pi%29=1 again.
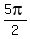
For example, sin%28pi%2F2%29=1=sin%28pi%2F2-2pi%29=sin%28pi%2F2%2B2pi%29 are three consecutive crests (maxima) in the wavy graph, at -3pi%2F2%29%29%29+%2C+%7B%7B%7Bpi%2F2 , and 5pi%2F2
and sin%28-pi%2F2%29=-1=sin%28-pi%2F2%2B2pi%29 are two consecutive minima, at -pi%2F2 and 3pi%2F2.
In between those extremes, the function takes the same values more often, once on the way up, and again on the way down.
For example sin%28pi%2F6%29=1%2F2=sin%285pi%2F6%29
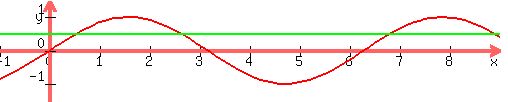
graph%28500%2C100%2C-1%2C9%2C-1.5%2C1.5%2Csin%28x%29%2C1%2F2%29
With a domain of all the real numbers as possible x values, the values of f%28x%29=sin%28x%29 repeat, so that function does not have an inverse.
For that reason, we define 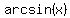arcsin%28x%29 as the inverse function of
f%28x%29=sin%28x%29 define on the domain -pi%2F2%3C=x%3C=pi%2F2
In that restricted domain, the only x that has sin%28x%29=1%2F2 is pi%2F6 .
The same goes for any other value of sin%28x%29 within the domain defined as -pi%2F2%3C=x%3C=pi%2F2.
The other inverse trigonometric functions are defined similarly.
y=arccos%28x%29 is the angle y such that
x=cos%28y%29 and 0%3C=y%3C=pi

Answer by DrBeeee(684) About Me  (Show Source):
You can put this solution on YOUR website!
Let
(1) sin(x) = y
Then
(2) x = arcsin(y)
Put y of (1) into (2) and see that
(3) x = arcsin(sin(x))
In your problem
(4) x = -3pi/5
So the exact value of
(5) arcsin(sin(-3pi/5)) = -3pi/5
When the exact answer is asked for, use the symbol, pi in this case, for the irrational number not a decimal.