Let the sides of the triangle be a, b, and c.
The altitudes are given in the ratio of 1:2:3.
So we can let x be such that the altitudes have lengths x,2x, and 3x.
Let x be the length of the altitude drawn to side a.
Let 2x be the length of the altitude drawn to side b.
Let 3x be the length of the altitude drawn to side c.
Now we use the usual formula for the area of a triangle, which is
Area of a triangle =  ·(any side of triangle)·(altitude drawn to that side)
Therefore
Area of the triangle =
·(any side of triangle)·(altitude drawn to that side)
Therefore
Area of the triangle =  a·x =
a·x =  b·2x =
b·2x =  ·3x
·3x
 a·x =
a·x =  b·2x =
b·2x =  c·3x
Multiply by 2
a·x = 2b·x = c·3x
ax = 2bx = 3cx
Divide by x
a = 2b = 3c
We are given that the perimeter is 36, so
P = a + b + c = 36
So we have the system
a = 2b
a = 3c
a + b + c = 36
Solve the first eq. for b: b =
c·3x
Multiply by 2
a·x = 2b·x = c·3x
ax = 2bx = 3cx
Divide by x
a = 2b = 3c
We are given that the perimeter is 36, so
P = a + b + c = 36
So we have the system
a = 2b
a = 3c
a + b + c = 36
Solve the first eq. for b: b =  Solve the second eq. for c: c =
Solve the second eq. for c: c = 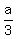 a +
a +  +
+ 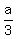 = 36
6a + 3a + 2a = 216
11a = 216
a =
= 36
6a + 3a + 2a = 216
11a = 216
a = 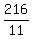 Then b =
Then b =  =
=  a =
a =  ·
·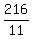 =
= 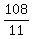 And c =
And c = 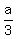 =
=  a =
a =  ·
·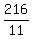 =
=  So the sides would have to be a=
So the sides would have to be a=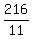 , b=
, b=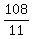 , c=
, c=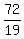 However, the sum of any two sides of a triangle must be greater than
the third side.
So those values are not possible sides for a triangle because b+c < a
So there is no possible solution. No triangle can have its altitudes in
the ratio 1:2:3.
Edwin
However, the sum of any two sides of a triangle must be greater than
the third side.
So those values are not possible sides for a triangle because b+c < a
So there is no possible solution. No triangle can have its altitudes in
the ratio 1:2:3.
Edwin