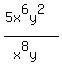SOLUTION: The expression {{{(5x^6y^2)/(x^8y)}}} is equivalent to what

Use the rule of subtracting exponents:

If an exponential factor of the numerator has the same base as an exponential
factor of the denominator, then

1. If the larger exponent is in the numerator, then subtract the exponent of
the denominator from the exponent in the numerator and place the resulting
exponential in the numerator, and eliminate the exponential from the
denominator.

2. If the larger exponent is in the denominator, then subtract the exponent of
the numerator from the exponent in the denominator and place the resulting
exponential in the denominator, and eliminate the exponential from the
numerator.

[In either case, subtract the smaller numerator from the larger and place
the resulting exponential where the larger exponent was, top or bottom]

Give the y the exponent of 1.



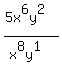Look at the exponentials  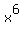in the numerator and  in the
denominator.  The larger exponent is in the denominator, so we subtract
the exponents "larger - smaller" = 8-6 = 2, and place the resulting 
exponential  in the denominator because the larger exponent 8
was in the denominator, and eliminate the 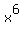 from the numerator:



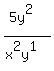Now look at the exponentials  in the numerator and  in the
denominator.  The larger exponent is in the numerator, so we subtract
the exponents "larger - smaller" = 2-1 = 1, and place the resulting 
exponential  in the numerator because the larger exponent 2
was in the numerator, and eliminate the  in the denominator:



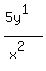Finally we don't need to write the 1 exponent, so we end up with:



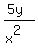Edwin