Question 808513: I have twice as many nickels as I do quarters. If together they add up to $4.90, how much quarters and nickels do I have? I need to write an equation that represents the problem and then solve it. Please help I can't figure it out, the equation is the hard part
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE ALGEBRA WAY:
 = number of nickels = number of nickels
 = number of quarters = number of quarters
"I have twice as many nickels as I do quarters" translates into

The phrase "together they add up to $4.90" translates into
 if you are thinking in cents, or if you are thinking in cents, or
 if you are thinking in $. if you are thinking in $.
Needless to say, I like  better, better,
but we could divide both sides of that equation by 5 and get a simpler equation:
 --> --> --> -->
From  you could multiply both sides times 20 to get the same result: you could multiply both sides times 20 to get the same result:
 --> --> }--> }-->
You end up with a system of two equations, one of them being  . .
If you simplified the other one, your system is

No matter what second equation you use, it is easy to substitute 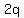 for for  in the second equation, and just have one equation to solve for just the variable in the second equation, and just have one equation to solve for just the variable  . .
I would use  and substituting and substituting 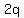 for for  would get would get
 --> -->  --> -->  --> --> 
After that you find that the number of nickels is 
Using  you would substitute to get you would substitute to get
 . .
Using  you would substitute to get you would substitute to get
 . .
If you have not been taught about systems of linear equations, you may be expected to directly figure out one of the equations with just  highlighted above, highlighted above,
and then solve it,
without mentioning a "system of linear equations".
If you have been taught about systems of linear equations,
you may be expected to use fancy wording and format,
maybe mentioning a "system of linear equations" that you solve "by substitution".
VERIFICATION:
Getting that many of each coin from a willing adult,
asking for help in verifying your solution from a younger sibling who has learned to count money,
and afterwards sharing the profits
would be a satisfying and profitable learning experience for all involved.
|
|
|