SOLUTION: Can i please get some assistance to solve a for the following equation? If possible may you please show me how to draw the answer on the number line? I would be so greatful! |a

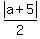 > 6

First you isolate the absolute value by multiplying
both sides by 2

|a + 5| > 12

Then you use whichever of these two rules applies:

Rules for getting rid of absolute value bars in inequalities:

----------------------------------------------
Rule for < or ≦ 


For  |mx+b| < c

If c is positive the inequality becomes

     -c < mx+b < c

Then you solve that with x in the middle.

If c is not positive there is no solution.

It's the same for ≦

--------------------------------------
Rule for > or ≧ 

For  |mx+b| > c

If c is positive the inequality becomes

mx+b < -c  OR  mx+b > c

Then you solve each of those for x and write "OR" between them

If c is not positive the solution is "ALL REAL NUMBERS"

It's the same for ≧ 

--------------------------------------------

Back to your problem

|a + 5| > 12

To get rid of the absolute value bars

Since 12 is positive the inequality becomes

a+5 < -12  OR  a+5 > 12
  a < -17  OR    a > 7

<=====)------(=====>
    -17   0  7

(-∞,-17) ᑌ (7,∞)

Edwin