Question 80689: I've been trying to figure a few of these equations all day, but I can't seem to understand the how to find the slopes and graphs and I'm getting more homework than I can keep up with. Also is there a more simple explanation of how to find whether points are parallel or perpendicular? Is there a way I can get some one on one tutoring, either from here or another program?
-find the slope of any line perpendicular to the line through points (0,5) and
(-3,-4)
-Floor plans for a building have the four corners of a room at the points (2,3),(11,6),(-3,18) and (8,21).
Determine whether the side through the points(2,3) and (11,6) is perpendicular to the sides through the points (2,3) and (-3,18).
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! First lets find the slope through the points (0,5) and (-3,-4)
note: check out this solver to get more help with finding the slope
Since the perpendicular slope is the negative inverse of the original slope, we can say the perpendicular slope is
 where where 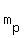 is the perpendicular slope is the perpendicular slope
So plug in m=3 to get

So the perpendicular slope is

---------------------------------------------------------------
"Floor plans problem"
First lets find the slope through (2,3) and (11,6)
Now lets find the slope through (2,3) and (-3,18)
Notice that the side that contains the points (2,3) and (11,6) has a slope of  . Also notice that the side containing (2,3) and (-3,18) has a slope of . Also notice that the side containing (2,3) and (-3,18) has a slope of  . So to see if they are perpendicular we simply invert and negate either slope. For instance, lets invert and negate the first slope . So to see if they are perpendicular we simply invert and negate either slope. For instance, lets invert and negate the first slope  : :


So the perpendicular slope is -3. This shows that -3 and 1/3 are perpendicular slopes which means the two sides are perpendicular.
|
|
|