Question 806203: Any help you could give on this problem would be great. Thank you!!!
For 0 degrees ≤ theta < 1080 degrees, find all values of theta such that cos theta = 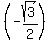 . .
I have discovered that all possible answers have to be in quadrant 2 (I THINK), because that is where the cosine is negative, but not both numerator and denominator of the number have to be negative (like they would in quadrant three). Knowing that cos theta is x/r, this allows you to know the x and r values, of 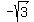 and 2, respectively. Then you can put them in the formula for r=2, of and 2, respectively. Then you can put them in the formula for r=2, of  , to find y as 1. I know that since 1080/360 is 3, there are three values, but this is as much information as I have been able to find. I am struggling to find the degree value for theta, and transfer the radians into something usable (if that makes sense). , to find y as 1. I know that since 1080/360 is 3, there are three values, but this is as much information as I have been able to find. I am struggling to find the degree value for theta, and transfer the radians into something usable (if that makes sense).
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are some values for sine and cosine that are easy to remember (no memorization required), and it is easy to remember the first quadrant angles they correspond to.
The values are 0,  , ,  , ,  , and 1. , and 1.
I'll explain later why they are easy to remember (at least for me).
We figure out problems for a "reference angle" in the first quadrant, and then "translate" the findings to other quadrants as needed.
 is a known reference angle and trigonometric function value. is a known reference angle and trigonometric function value.
Cosine has the same sign as  in all quadrants, so negative cosines are found in quadrants II and III. in all quadrants, so negative cosines are found in quadrants II and III.
Angles in quadrant II have the same sine and opposite cosine as their supplements, who are in quadrant I.
 . .
Angles in quadrant III have the opposite sine and cosine as their  smaller first quadrant reference angles. smaller first quadrant reference angles.
So  . .
So far we have found the angles that have  in the first turn, in the first turn,  . .
There are no answers in quadrants I and IV, where cosine is positive, and the values for cosine (or for any other trig function) do not repeat within a quadrant, so  and and  are the only solutions for are the only solutions for  . .
As you said, there are 3 whole  turns in turns in 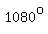 , and since cosine has a period of , and since cosine has a period of  , the same cosine values are repeated for angles , the same cosine values are repeated for angles  and and 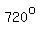 larger. larger.
That gives us 4 more answers:
 , ,
 , ,
 , and , and
 . .
You could express all the answers as
 for for  an element of {1, 2, 3} , if you wanted to look fancy. (That is kind of formula is what you have to use if they ask you for all the angles an element of {1, 2, 3} , if you wanted to look fancy. (That is kind of formula is what you have to use if they ask you for all the angles  , no matter how large). , no matter how large).
HOW TO KNOW THE VALUES LISTED AT THE TOP:
Below is an equilateral triangle with sides measuring 1. Drawing an altitude, we split that triangle symmetrically into two congruent right triangles.
The angles in the equilateral triangle measure  , and the altitute split one of them into two , and the altitute split one of them into two  angles. angles.
The hypotenuse of one of those right triangles measures 1, because it is the side of the equilateral triangle.
The short leg of one of the right triangles measures  , because it is half of a side of the equilateral triangle. , because it is half of a side of the equilateral triangle.
According to the Pythagorean theorem, the long leg measures
 . .
The  length of the short leg, opposite the length of the short leg, opposite the  angle and adjacent to the angle and adjacent to the  angle is angle is

The  length of the long leg, opposite the length of the long leg, opposite the  angle and adjacent to the angle and adjacent to the  angle is angle is

 No need to memorize without understanding, and you can recalculate those values if you forget them. No need to memorize without understanding, and you can recalculate those values if you forget them.
Now, consider a square with side length 1, and its diagonal 
The diagonal splits the square into two isosceles right triangles, with 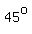 angles opposite legs og length 1. angles opposite legs og length 1.
According to the Pythagorean theorem, the hypotenuse measures

So, the value for sine and cosine of those 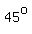 angles are the ratio of leg to hypotenuse: angles are the ratio of leg to hypotenuse:

MORE:
Trigonometric functions are often defined as the coordinates of a point determined by the angle in "standard position" and the "unit circle:
   are the coordinates of point B. are the coordinates of point B.
 and and  are the coordinates of point C are the coordinates of point C
|
|
|