Question 805960: An isosceles triangle has a perimeter of 24. The sum of the equal sides must be greater than the third side. What are the possible lengths of the sides?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! If the side length have to be integers, these are the options:
The unequal side length could be  , and each of the other sides could measure 
The unequal side length could be  , and the other sides could measure  each
The unequal side length could be  , and the other sides could measure  each
The unequal side length could be  , and the other sides could measure each
The unequal side length could be , and the other sides could measure  each.
The unequal side length could not be  , with the other sides measuring  each, because  , and the triangle has collapsed, flatlined. The 3 points that would have been the vertices are all on the same line.
The sum of the lengths of the equal sides is not greater than the length of the third, unequal side.
If we do not stick to integers, the options are unlimited, infinite, endless.
The unequal side length could be 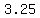 ,  ,  , or anything else you can think of (as long as it is less than 12).
The set of real numbers is "dense", meaning that in between two real numbers, no matter how close, you can always find another real number.
Maybe your teacher expects just the unequal side length to be an integer.
Arbitrary, but we must always cater to the teacher (if we care about grades).
In that case, there are more options.
The unequal side could measure  , and the other two sides would measure  ;
the unequal side could measure  , and the other two sides would measure  ,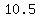
and so on.
|
|
|
