Question 805709: how to find all the zeros for
f(x)= 3x^4-11x^3-x^2+19x+6
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
If that polynomial has any rational zeros,
they are fractions of the form  or or 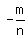
with  = a factor of = a factor of  (the independent term}, (the independent term},
and  = a factor of = a factor of  (the leading coefficient). (the leading coefficient).
That would suggest to try
 , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , and , and 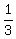 and and  . .


That means  is a zero of is a zero of  , ,
and  is divisible by is divisible by  . .
We divide and find
 <---> <---> 
Next easier to try would be  and and  . .
WE can try to calculate 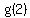 or try to divide or try to divide 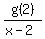 , ,
but either way, we find that
 and and  <---> <--->
 is a quadratic polynomial that can be easily factored as is a quadratic polynomial that can be easily factored as

(If we did not figure out a factoring, we could use the quadratic formula to find the zeros of the  anyway). anyway).
In sum,
 so the zeros are the values that make each of those four binomial factors equal to zero: so the zeros are the values that make each of those four binomial factors equal to zero:
 , ,
 , ,
 , ,
and 
|
|
|