SOLUTION: Solve each of the following systems of linear inequalities graphically. 10. 3x – y < 6 X > 1 Y < 3

Solve each of the following systems of linear 
inequalities graphically. 
10.

3x – y < 6
x > 1
y < 3

First form the three equations of the boundary lines.
These are formed by replacing each inequality symbol
by an equal sign. The equations of the boundary lines
are 

3x – y = 6
     x = 1
     y = 3

Now we draw the equation of the first boundary line,

3x - y = 6. It's intercepts are (0,-6) and (2,0):

 

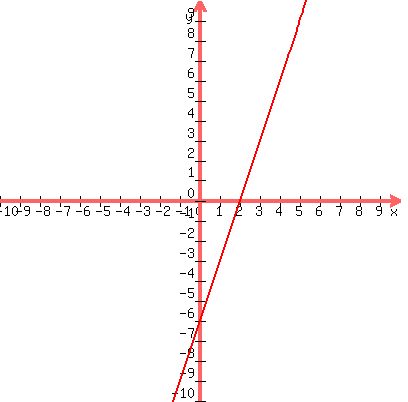It should be a dotted line, not a solid line.
I cannot draw dotted lines on here, but you can on
your paper.

But now before drawing the second line we must decide
which side of this boudary line the solutions to the
corresponding inequality the solutions are on. To do
this we arbitrarily select any point that DOES NOT lie 
on the boundary line as a test point. 

Suppose we choose the point (-3,5) as a test point.

 

Now we substitute (-3,5) into the inequality

   3x – y < 6
3(-2) - 5 < 6
   -6 - 5 < 6
      -11 < 6

This is true, so its solutions lie on the
same side of the boundary line that the test 
poin was on.  Therefore we make some marks
along that side of the line:

 

Now we're ready to draw the next boundary
line, x = 1. This is a vertical line that
intersects the x axis at 1. Again it
should be a dotted line, and you should
draw it dotted on your paper:



We can use the same test point we used for the
first line since it is not on the line.
So we substitute (-3,5) into the inequality.
Not that we need only substitute the x-value
since there is no place to substitute the y
value.  That is prefectly OK:

        x > 1
       -3 > 1

This is false, so its solutions lie on the
OPPOSITE side of the boundary line that the test 
poin was on.  Therefore we make some marks
along the RIGHT side of the green line:

 

Now we're ready to draw the next boundary
line, x = 1. This is a vertical line that
intersects the x axis at 1. Again it
should be a dotted line, and you should
draw it dotted on your paper:



Now we're ready to draw the last boundary
line, y = 3. This is a horizontal line that
intersects the y axis at 3. Again it
should be a dotted line, and you should
draw it dotted on your paper:



We can use the same test point we used for the
other two lines since it is not on this line
either. So we substitute (-3,5) into the inequality.
Not that we need only substitute the y-value
since there is no place to substitute the y
value.  That is prefectly OK:

        y < 1
        5 < 1

This is false, so its solutions lie on the
OPPOSITE side of the boundary line that the test 
poin was on.  Therefore we make some marks
along the LOWER side of the blue line:



Now we see that the solution set is the region
which is on the same sides of all three lines
which the X's are on.  So the triangle region
is the solution.  You should shade that solution.
I can't shade the triangle on here but you can on
your paper.  Also don't forget to draw the lines 
dotted and not solid.  You should draw them
solid only when the inequality is either <
or >, but dotted for > or <.

Another comment:  The easiest point to choose
as a test point is NOT the point I chose,
(-3,5)!!  A much easier test point to choose is
the origin (0,0).  The origin may be chosen
as a test point any time the boundary line does 
not pass through the origin.  The reason I did 
not choose the origin here as a test point was
to show you that the choice of test points is 
really arbitrarily. If I had chosen the origin 
each time, you might have thought you always 
had to choose the origin, and would not know
what to do if you ran into a problem where a
boundary line passed through the origin. 

Edwin