cos(4x)=0
The angles with cosine 0 are all the odd multiples of  4x =
4x = 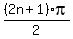 x =
x = 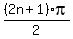 ÷4
x =
÷4
x = 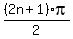

 x =
x = 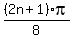
 Divide all three sides by p
Divide all three sides by p
 Multiply all three sides by 8 to clear of fractions:
Multiply all three sides by 8 to clear of fractions:
 Subtract 1 from all three sides
Subtract 1 from all three sides
 Divide all three sides by 2
Divide all three sides by 2
 Since n is an integer
Since n is an integer
 ,
n ∈ {4,5,6,7}
Answers: x =
,
n ∈ {4,5,6,7}
Answers: x =  =
= 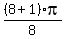 =
= 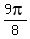 x =
x =  =
=  =
=  x =
x =  =
= 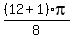 =
=  x =
x =  =
= 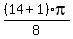 =
= 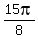 Edwin
Edwin