Question 803391: Which result is correct?


a) 





b) 


Where is the mistake?
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I see no mistake in b), and it seems to be the most direct way to the answer.
In a), I believe that the problem is that
 means that means that

I see those parentheses around 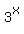 as crucial to establish the proper meaning of the expression. as crucial to establish the proper meaning of the expression.
Certainly, 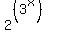 is not the same as is not the same as  as you assumed to keep on going. as you assumed to keep on going.
If  , ,  , ,
while 
Probably there are rules about order of operations that assign one or another meaning to  , but I would forget them soon after reading them, because those expressions do not come up too often, so I will use parentheses to make my meaning clear. , but I would forget them soon after reading them, because those expressions do not come up too often, so I will use parentheses to make my meaning clear.
In any case, I would not know how to proceed further after getting to 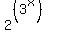 , because I do not know of any equivalent expression. , because I do not know of any equivalent expression.
|
|
|