SOLUTION: If 9^x-1 = 7 then what is 3^2x+3 The ^'s mean exponent and the 2x+3 at the end is ALL part of the exponent of 3. So it should belike 3 TO THE POWER OF "2x+3"

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: If 9^x-1 = 7 then what is 3^2x+3 The ^'s mean exponent and the 2x+3 at the end is ALL part of the exponent of 3. So it should belike 3 TO THE POWER OF "2x+3"      Log On


   

Question 803297: If 9^x-1 = 7 then what is 3^2x+3
The ^'s mean exponent and the 2x+3 at the end is ALL part of the exponent of 3. So it should belike 3 TO THE POWER OF "2x+3"
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
(Note: much of the rendering below did not show well.)

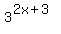
If 9%5Ex-1+=+7 then what is 3%5E%282x%2B3%29
Without the rendering tags, 9^x-1=7 and 3^(2x+3).


Solve for x in the first equation, and then just use the value in the expression you want evaluated.

9%5Ex-1=7
9%5Ex=7%2B1
9%5Ex=8
Choosing base 10 logarithms, log%2810%2C9%5Ex%29=log%2810%2C8%29
x%2Alog%2810%2C9%29=log%2810%2C8%29
x=log%2810%2C8%29%2Flog%2810%2C9%29, which is how we use it. Ratio of logarithms has no special law.

You would want to evaluate, or compute 3%5E%282%2A%28log%2810%2C8%29%2Flog%2810%2C9%29%29%2B3%29
3^(2*(log(10,8)/log(10,9))+3)

Slightly modified or split as 3%5E%282%2Alog%2810%2C8%29%2Flog%2810%2C9%29%29%2A3%5E3
3^(2*log(10,8)/log(10,9))*3^3

'
3%5E%282%2A0.90309%2F0.95424%29%2A27
3^(2*0.90309/0.95424)*27

3^(2*0.90309/0.95424)*27



8.00004%2A27
highlight%28216%29

Somehow, this should be simpler to do, seeing that kind of last two steps.
The rendering may unfortunately not display thoroughly.