Question 802751: 4x + 3y greater than or equal to 30
x + 3y greater than or equal to 21
x greater than or equal to 0 , y greater than or equal to 0
minimum for: C = 5x + 8y
x + y greater than or equal to 8
x + 5y greater than or equal to 20
x greater than or equal to 0, y greater than or equal to 0
Minimum for: C = 3x + 4y
1. Rewrite the constraints in slope-intercept form
2. List all vertices of the feasible region as ordered pairs.
3. List the values of the objective function for each vertex.
4. List the maximum or minimum amount, including the x, and y-value, of the objective
function.
I am stuck in this two questions I really do not know how to do them.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! For the first problem, the constraints are:
 , 
The objective function and goal are:
minimum for: C = 5x + 8y
Following the step-by-step instructions:
1) The boundary lines to put in slope-intercept form are
 -->  -->  and
 -->  -->  , because
 does not have a slope, and
there is nothing to change in  , with  .
Maybe you were expected to make the inequalities into something that we could call slope-intercept form:
-->  -->  and
-->  --> 
2) You need to graph (or at least sketch) the feasible region satisfying all those constraints.
means the line and all points above it.
means the line and all points above it.
 means the line (the x-axis) and all points above it.
 means the line (the y-axis) and all points to the right of the y-axis.
The feasible region is the bubbly region at right  and the blue bubbles mark the vertices.
The vertices are the points where the boundary lines cross at the edges of the feasible region:
 -->  --> 
 or better  -->  --> 
 or better  -->  --> 
3) 
At A(0,10), 
At B(3,6), 
At C(21,0), 
4) The minimum is  at point
The second problem is solved similarly:
The boundary lines are
 ,  , and the x and y-axes
 --> 
 --> 
The vertices of the feasible region are:
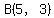 , the solution to  ,
 , the solution to  , and
 , the solution to 
The objective function is  and the values at the vertices of the feasible region are:
At A, 
At B, 
At A, 
The minimum is  at point 
|
|
|
