Question 802064: The midpoints of each side of an equilateral triangle are joined forming a smaller triangle. The midpoints of this smaller triangle are then joined, forming a third triangle and so on. If the length of each side of the original triangle is one, what is the total perimeter of all the triangles that can be formed this way?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The sides of each triangle will be  as long as the sides of the prior triangle, so the first perimeter is  , the second is  , the next  , and so on.
The perimeters form a geometric sequence.
The sum converges to  .
That is easy to see because as you add each perimeter you are reducing the difference between your sum and  by a factor of  .
If you need to show your work, you could dust all those formulas about geometric sequences, and use the version taught in your class.
Maybe you would use the fact that the sum of the first  terms of a geometric sequence is
where  is the first term and  is the common ratio.
In this case  and  , so
As increases without bounds,  approaches zero, and  approaches .
Maybe you were taught that if  an infinite geometric series converges to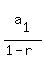 
In that case, plugging and into that formula you get that the sum of the infinite series is 
|
|
|
