Question 800855: Calculate the following problem: suppose you offered to put a penny into your child’s piggy bank. Then, each day forward you put in double the amount from the previous day. How many days would it take to make $100,000? (Day 1 = 1 penny, Day 2 = 2 pennies, Day 3 = 4 pennies, Day 4 = 8 pennies, Day 5 = 16 pennies, Day 6 = 32 pennies, and so on) Remember to add the contribution from each previous day to find the total amount of pennies at the end of the day. (Day 2 = total 3 pennies, Day 3 = total 7 pennies, and so on)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! $100,000 is 10,000,000 pennies, which I can write as 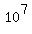 pennies. pennies.
The numbers of pennies added to the child's piggy bank form a geometric sequence.
In a geometric sequence with first term  and common ratio and common ratio 
the general form for term number  is is  , ,
and the sum of the first  terms can be calculated as terms can be calculated as

In this case  and and  , so , so

For  we need we need  , which we can state as , which we can state as 
I happen to know that 
That means that 
so after 20 days the child's piggy bank would not have $100,000.

so after 23 days the child's piggy bank would not have $100,000.

so the child's piggy bank would get over $100,000 on day 
NOTE:
I just weighed 50 pennies, and got a weight of 131 g, so  pennies would weigh about 260 g = 0.26 kg. pennies would weigh about 260 g = 0.26 kg.
Then  pennies would weigh about pennies would weigh about  kg. kg.
That's 26 metric tons. You would need a large truck to carry that many pennies.
|
|
|