SOLUTION: I have a problem that I need to solve finding all solutions in [0,2pi) 2 cos x + 2 sin x = sqrt2 how do i solve this problem

2cos(x) + 2sin(x) = √2

Divide every term by 2:

  cos(x) + sin(x) = 

We can make the left side into the form sin(A+B)=sin(A)cos(B)+cos(A)sin(B),
using the fact that sin() = cos( =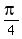 

Since all three of those are equal, multiply the first term by the first
expression, the second term by the second expression and the term on the
right side by the third expression:

sin()cox(x) + cos()sin(x) = 

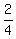sin() = 

sin() = 

The sine is positive in QI and QII, so

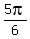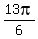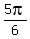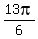    + x = , , , etc.  

                x = 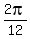-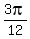, 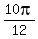-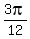, -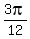, etc.  

                x = -, -, -, etc.

                x = 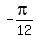, , , 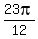etc.    

Ignore the 1st one since it is not in [0,2p),

Solution:  ,  

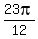Edwin