SOLUTION: sketch the region {{{y=sqrt(sin(x))}}} and above {{{y= 2*x/pi}}} in the first quadrant. Find the lower intersection point ,a, and the upper section, b,. Hello, im not sure how t

Algebra ->  Coordinate-system -> SOLUTION: sketch the region {{{y=sqrt(sin(x))}}} and above {{{y= 2*x/pi}}} in the first quadrant. Find the lower intersection point ,a, and the upper section, b,. Hello, im not sure how t      Log On


   

Question 798894: sketch the region y=sqrt%28sin%28x%29%29 and above y=+2%2Ax%2Fpi in the first quadrant. Find the lower intersection point ,a, and the upper section, b,.
Hello, im not sure how to calculate this with a and b variables. I am confused how to solve this mathematically. I would appreciate any help for this problem. thx
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Here are the graphs of red%28y=sin%28x%29%29, green%28sqrt%28sin%28x%29%29%29, and blue%28y=2x%2Fpi%29
graph%28300%2C300%2C-0.2%2C1.8%2C-1.5%2C1.5%2Csin%28x%29%2Csqrt%28sin%28x%29%29%2C2x%2Fpi%29 blue%28y=2x%2Fpi%29 graphs as a straight line through the origin.
For x=0, y=2%2A0%2Fpi=0.
For x=pi%2F2, y=2%2A%28pi%2F2%29%2Fpi=pi%2Fpi=1.

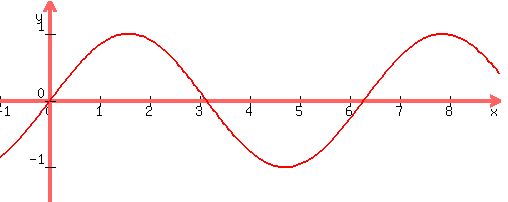
red%28y=sin%28x%29%29 graphs as the wavy curve we all know, graph%28500%2C200%2C-1%2C9%2C-1.5%2C1.5%2Csin%28x%29%29
with y=sin%280%29=0 for x=0,
and y=sin%28pi%2F2%29=1 for x=pi%2F2.

So y=2x%2Fpi and y=sin%28x%29 cross at (0,0) and at (pi%2F2,0).

y=sqrt%28sin%28x%29%29 exists wherever sin%28x%29%3E=0 and crosses y=sin%28x%29 when x=0 --> sin%28x%29=0 --> sqrt%28sin%28x%29%29=0, and
when x=pi%2F2 --> sin%28x%29=1 --> sqrt%28sin%28x%29%29=1.
Those are the same points where y=sin%28x%29 and y=2x%2Fpi cross. All 3 graphs cross at those points.
In between, 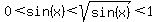0%3Csin%28x%29%3Csqrt%28sin%28x%29%29%3C1, so the graph for y=sqrt%28sin%28x%29%29 is above the graph of y=sin%28x%29.