|
Question 798831: divide 57 into two parts whose product is 782
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! I see two ways to find the answer: through a prime factorization, and by solving a quadratic equation. Solving a quadratic equation will find those two numbers, even if they are irrational or complex. Factoring will find them if they are integers (as the problem suggests).
If 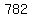 had been easier to factorize, I would have started by writing the prime factorization.
However, the number did not cooperate.
782 ÷ 2 = 391 was a good start, but 391 does not divide evenly by 2, 3, 5, 7, or 11.
The next step would have been trying prime numbers up to 19 to see if one of them would divide 782 evenly.
I did not need to go past 19 because
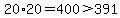
so if a number equal or larger than 20 was a factor of 19, the other factor would be a smaller number.
If I had had the patience to try the next prime numbers (13, 17, and 19), I would have found that
391 ÷ 17 = 23,
and that would have given me the prime factorization for 782 as
From there, I would know that the more promising products were
 and that
Adding the factors in those two products,
 and  ,
I would have found the solution as  with  .
Solving a quadratic equation:
 <-->  is an equation with  and  as solutions.
If  and  , I can find  and  as solutions of 
Solving that equation by factoring means finding the factors as explained above.
Solving it by "completing the square" would require complex calculations plus thinking.
On the other hand, the quadratic formula required no thinking, so I reluctantly reached for the calculator to use the quadratic formula.
The quadratic formula says that
gives the solutions to  .
For ,  ,  , and  ,
so the solutions will be given by
 .
That gave me the two solutions as
 and 
Factoring was easier. I should practice patience.
|
|
|
| |
