Question 798189: A company sells running shoes to dealers at a rate of $34 per pair if fewer than 70 pairs are ordered. If a dealer orders 70 or more pairs (up to 600), the price per pair is reduced at a rate of 5 cents times the number ordered. What size order will produce the maximum amount of money for the company?
So far I have... $34 if x<70 and 70>or equal to -.05x < 600
thankyou
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you need to show work, just write:


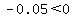 so maximum at so maximum at 
UNDERSTANDING THE PROBLEM:
The price per pair of running shoes is
$ if if  or or
$ if if 
They must be sure their customers will not place large orders, because for an order of 600 pairs, the price per pair would be
$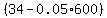 = $ = $ = $ = $
Anyway, if the company sells  pairs, between 70 and 600 pairs ( pairs, between 70 and 600 pairs ( ), they get ), they get
$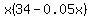
The amount (in $) they get, as a function of  , is a quadratic function: , is a quadratic function:
 or or 
For this problem, that function is only defined for some values of  , ,  . (The domain of that function is restricted by . (The domain of that function is restricted by  ). ).
The function  without restrictions graphs as a parabola, without restrictions graphs as a parabola,
a nicely symmetrical curve, with a maximum exactly halfway between the zeros,
which are at  , ,
and where  <--> <-->  <--> <-->  <--> <-->  . .
So that maximum is at exactly  . .
Easy. No memorized formulas required.
WHAT IS EXPECTED:
Your teacher may expect you to multiply to get from
 to to  , ,
and then apply memorized facts and formulas.
You've been taught the fact that a quadratic function 
has a maximum or minimum at  , ,
which is a maximum if  , and is a minimum if , and is a minimum if  . .
In this case  , so there is a maximum, , so there is a maximum,
and  calculates as calculates as 
|
|
|