Question 798186: A concrete walk of uniform width is to be built around a circular pool, as shown in the figure. The radius of the pool is 16 meters, and enough concrete is available to cover $ {\color{black}144} \pi $ square meters. If all the concrete is to be used, how wide should the walk be?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! PROBABLE EXPECTED SOLUTION:
The area of the pool is the area of a circle of radius 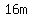 , so it is , so it is
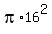  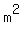
The area (in square meters) of the pool plus a surrounding walkway of width  meters would be the area of a circle of radius meters would be the area of a circle of radius 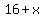 meters: meters:

The difference is the area of the walkway. In square meters, it is

If we can use enough concrete to cover 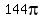 square meters, square meters,

and  is our equation. is our equation.
We can solve it by completing the square, by factoring, or by using the quadratic formula.
Completing the square:





Since we are looking for a positive number  , ,
 --> -->  --> --> 
Factoring:


 --> -->  --> --> 
because  <--> <-->  is not an acceptable solution. is not an acceptable solution.
Applying the quadratic formula:
The solutions to  are given by are given by 
In the case of  , ,  , ,  , and , and  , so , so

The two solutions are
 which does not make sense as width of a walkway, which does not make sense as width of a walkway,
and  which is the width, in meters, of the walkway we want. which is the width, in meters, of the walkway we want.
MENTAL MATH QUICK SOLUTION:
The area of a circle or radius  is is 
The area of the pool, 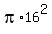 square meters, square meters,
plus the area of the walkway,  square meters, square meters,
adds up to the area,  , of a larger circle of radius , of a larger circle of radius  meters. So meters. So  --> --> 
That reminds me of the Pythagorean theorem.
Since  and and  , I can think of , I can think of  as as
 --> -->  --> --> 
Since  has been used in so many problems, I remember it better than I remember the times tables, so has been used in so many problems, I remember it better than I remember the times tables, so
 --> -->  --> -->  --> --> 
and that means that the width of the sidewalk is  meters meters
|
|
|