SOLUTION: (a) The coordinates of the points P and Q are (6,4) and (-2,0) respectively. T is the point on PQ such that PT over TQ equals r. Write down the coordinates of T in terms of r. (

Algebra ->  Length-and-distance -> SOLUTION: (a) The coordinates of the points P and Q are (6,4) and (-2,0) respectively. T is the point on PQ such that PT over TQ equals r. Write down the coordinates of T in terms of r. (      Log On


   

Question 798046: (a) The coordinates of the points P and Q are (6,4) and (-2,0) respectively. T is the point on PQ such that PT over TQ equals r. Write down the coordinates of T in terms of r.
(b) Given two lines L(1): x+7y-23=0 and L(2): 5x-4y+15=0. Find the equation of the line L(3) passing through the intersection of L(1) and L(2) and perpendicular to PQ.
(c) Using the result of (a) or otherwise, find the ratio in which L(3) divides PQ.
Please help me! I don't really understand!
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Part (c) is not clear. Part (a) does not ask for an exact numeric answer. Part (b) seems clear enough.

Part (b):
Find the intersection, a point, of L1 and L2. Find the slope of PQ and determine the slope of a perpendicular line to PQ. Use the point-slope form for a line with this slope and point of intersection of L1 and L2 to find the equation for the line.


L1: x+7y=23
L2: 5x-4y=-15

L1 is also 5x%2B35y=5%2A23, or 5x%2B35y=115.
L1-L2 is %285x%2B35y%29-%285x-4y%29=115-%28-15%29, 39y=130, y=13%2A10%2F%283%2A13%29, y=10%2F3
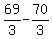From L1, x=23-7y, so x=23-7%2810%2F3%29, x=23%2A3%2F3-70%2F3, 69%2F3-70%2F3, x=-1%2F3
Intersection of L1 and L2 is at x=-1%2F3, y=10%2F3.

Slope of PQ: %284-0%29%2F%286-%28-2%29%29=1%2F2.
A line perpendicular to PQ must have a slope of -2.

The line perpendicular to PQ and containing the point (-1/3, 10/3) is, using the point-slope form, y-10%2F3=-2%28x-%28-1%2F3%29%29
y-10%2F3=-2x-2%2F3
3y-10=-6x-2
6x%2B3y=10-2
6x%2B3y=8 Standard Form; or if you prefer, 6x%2B3y-8=0