SOLUTION: find the general equation of ellipse with center at (1,5), major axis parallel to x-axis, length of latus rectum is 9/4, distance between foci is 2squareroot of 55 units.

 


We will let P and S be the foci.

For the above we are given:

O = center = (1,5)
QR = TU = latus rectum = 
SP = distance between foci = 2√55

So we can deduce that:

OP = c = SP = √55

P = (1+√55,5)
PQ = QR =  =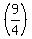 
Q = (1+√55,5+)

The standard equation of the ellipse, since it has major axis horizontal is



To avoid so many fractions we will clear of fractions:

b²(x-h)² + a²(y-k)² = a²b²

b²(x-1)² + a²(y-5)² = a²b²

Since we know that the ellipse passes through the point Q = (1+√55,5+),

b²(1+√55-1)² + a²(5+-5)² = a²b²

b²(√55)² + a²()² = a²b²

b²(55) + a²() = a²b²

Multiplying through by 64:

3520b² + 81a² = 64a²b²

We know that all ellipses have the property

c² = a²-b²

and since c = √55, c² = 55

a²-b² = 55 

So we have the system of equations:

3520b² + 81a² = 64a²b²
a²-b² = 55

Solve the second equation for a²,  a²=55-b²

Substituting that in the first:

  3520b² + 81(55+b²) = 64(55+b²)b²

3520b² + 4455 + 81b² = 3520b² + 64b4
 -64b4 + 81b² + 4455 = 0
  64b4 - 81b² - 4455 = 0
    (b²-9)(64b²+495) = 0 
     b²-9 = 0;  64b²+495 = 0
       b² = 9;  64b² = -495     
        b = 3;    b = imaginary (ignore)

Substitute b=3 in a²-b² = 55

a²-b² = 55
a²-3² = 55
 a²-9 = 55
   a² = 64
    a = 8

If we wanted the standard equation, it would be:







But we want the general equation,
not the standard, so we substitute in:

       b²(x-h)² + a²(y-k)² = a²b²
        9(x-1)² + 64(y-5)² = 64·9
9(x²-2x+1) + 64(y²-10y+25) = 576
9x²-18x+9 + 64y²-640y+1600 = 576
    9x²+64y²-18x-640y+1609 = 576
    9x²+64y²-18x-640y+1033 = 0

Edwin