Question 798014: Can you please help me solve this simultaneous equation by substitution method?
x+y=0.5
x-y=1
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
To solve a system of equations by substitution, you start by solving one of the equations for one of the variables.
In this case, we could solve  for for  : :
 --> -->
Next, you substitute the expression found for that variable into the other equation.
In this case, we replace 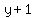 for for  in in  to get to get

Then, you simplify and solve the resulting equation:
 --> --> --> --> --> --> --> --> --> -->
Finally, you go back to the equation initially "solved" and plug in the value found:
Plugging  into into  we find we find
 --> -->
The solution to the system of equations is

It is good practice to verify that your solution is correct by plugging the numbers found into the original equations.
Sometimes the problem instructions tell you to check that way.
Plugging  and and  into into  we find we find
 <--> <--> , which is true. , which is true.
Plugging the solution found into  we find we find
 <--> <--> , which is also true. , which is also true.
Now we know that the solution found is correct. We did not make a mistake.
NOTE:
It is not always that easy. To start, you should choose wisely what variable to solve for. Look for a variable that has no visible coefficient in front.
Otherwise, you may end up working with fractions, and it is more likely to make a mistake.
If the system is  , ,
the easiest way to start is to solve  for for  : :
 --> --> . .
|
|
|