Question 797445: Find all vertices. Find Minimum or Maximum value.
{x+y<=6
{2x+y<=10
{x>=o,y>=0
{Maximum: P=4x+y
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website!  includes the line  and all the point to one side of that line.
What side?
Obviously the side with the origin (0,0), because  is a solution.
The line obviously passes through the points (6,0) and (0,6) because
 --> --> and
 --> -->
 includes the line  and all the point to one side o fthat line.
What side?
Obviously the side with the origin (0,0), because  is a solution.
The line obviously passes through the points (5,0) and (0,10) because
--> --> and
--> --> --> -->
 includes the line (the y-axis) and all the points to the right of it, like (1,0), with  that satisfy  .
 includes the line (the x-axis) and all the points above it, like (0,1), with  that satisfy  .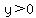
The space that satisfies all those constraints is the quadrilateral OABC below.
 The maximum value for P is at a vertex or along one entire edge of that quadrilateral.
Point B is the solution to  , which is obviously  .
The value of 
at O(0,0) is  ;
at A(0,6) is  ;
at B(4,2) is  ; and
at C(5,0) is 
So the maximum is  at C(5,0).
|
|
|
