SOLUTION: A two digit number is 18 less than the sum of the squares of its digits. How many such numbers are there?

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: A two digit number is 18 less than the sum of the squares of its digits. How many such numbers are there?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 796205: A two digit number is 18 less than the sum of the squares of its digits. How many such numbers are there?
Found 2 solutions by KMST, MathTherapy:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
You can try to narrow your choices looking at issues of divisibility and/or modular arithmetic.
Alternatively, there is the straight algebra approach.
I have a feeling that there is a much simpler solution out there, but I will co with my complicated one, because that's all I could think of.

STRAIGHT ALGEBRA:
a= tens digit (1%3C=a%3C=9)
b= ones digit 0%3C=b%3C=9
10a%2Bb= value of the number
"A two digit number is 18 less than the sum of the squares of its digits" translates as
10a%2Bb=a%5E2%2Bb%5E2-18
Here comes the algebra.
10a%2Bb=a%5E2%2Bb%5E2-18
a%5E2%2Bb%5E2-10a-b=18
a%5E2-10a%2B25%2Bb%5E2-b%2B1%2F4=18%2B25%2B1%2F4
%28a-5%29%5E2%2B%28b-1%2F2%29%5E2=173%2F4
4%28a-5%29%5E2%2B4%28b-1%2F2%29%5E2=173
highlight%28%282a-10%29%5E2%2B%282b-1%29%5E2=173%29
Since 0%3C=b%3C=9 , 0%3C=2b%3C=18, and highlight%28-1%3C=2b-1%3C=17%29
Since 1%3C=a%3C=9 , 2%3C=2a%3C=18, and 2-10=highlight%28-8%3C=2a-10%3C8%29=18-10.
There are only 5 possible values for 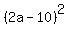%282a-10%29%5E2, and 4 of then do not lead to a solution.
abs%282a-10%29=0-->%282a-10%29%5E2=0-->%282b-1%29%5E2=173 has no solution with integer b such that 0%3C=b%3C=9
abs%282a-10%29=4-->%282a-10%29%5E2=16-->16%2B%282b-1%29%5E2=173-->%282b-1%29%5E2=173-16-->%282b-1%29%5E2=157 has no solution with integer b such that 0%3C=b%3C=9
abs%282a-10%29=6-->%282a-10%29%5E2=36-->36%2B%282b-1%29%5E2=173-->%282b-1%29%5E2=173-36-->%282b-1%29%5E2=137 has no solution with integer b such that 0%3C=b%3C=9
abs%282a-10%29=8-->%282a-10%29%5E2=64-->64%2B%282b-1%29%5E2=173-->%282b-1%29%5E2=173-64-->%282b-1%29%5E2=13709 has no solution with integer b such that 0%3C=b%3C=9

The only solution comes from abs%282a-10%29=2:
abs%282a-10%29=2-->%282a-10%29%5E2=4-->4%2B%282b-1%29%5E2=173-->%282b-1%29%5E2=169-->abs%282b-1%29=13
but as -1%3C=2b-1%3C=17, the only solution requires 2b-1=13--> 2b=14-->b=14%2F2-->highlight%28b=7%29
In turn,
abs%282a-10%29=2-->system%282a-10=-2%2C%22or%22%2C2a-10=2%29-->system%282a=8%2C%22or%22%2C2a=12%29-->system%28highlight%28a=4%29%2C%22or%22%2Chighlight%28a=6%29%29
So the two-digit number is highlight%2847%29 or highlight%2867%29.

CONSIDERING DIVISIBILITY:
18=2%2A9
Let's consider divisibility by 2 and by 9.

The number could be even, with both digits being even, making their squares, the sums of the squares, and the sum of the squares minus 18 even.
It cannot be even with an odd tens digit, because that would make that digit's square, the sum of the squares, and the sum of the squares minus 18 odd.
It cannot be odd with both digits being odd, because each square would be odd, making their sum even, and the sum of the squares minus 18 even.
The number could be odd if the tens digit is even.
Divisibility by 2, requires that the number be even with two even digits, or else odd, with an even first (tens) digit. Either way, the first digit must be even.

If a number is divisible by 9, when divided by 9, the remainder is zero, and the number can be written as 9k for some non-negative integer k, as in
0%5E2=0, 3%5E2=9, 6%5E2=36, and 9%5E2=81.
In that case the number is called congruent with 0 modulo 9, and all those numbers congruent with 0 are called congruent with one another.

Other numbers have a remainder of 1, 2, 3, ...., or 8, when divided by 9, and are called congruent modulo 9 with that remainder.
All the numbers with the same remainder and congruent modulo 9 with one another and with that remainder.
An easy way to find that remainder is to add the digits of the number. If the result is 10 or more, you keep adding the digits of the result, until you get a one digit number. if it is 9, then the remainder is zero. Otherwise, the final result is your remainder. So, if the digits are x and y, the number is congruent with x%2By modulo 9.

Since their difference is 18=2%2A9, congruent modulo 9 with zero,
the sum of the squares, and the sum of the digits must be congruent modulo 9.
The square of a digit minus the digit itself, x%5E2-x=x%28x-1%29 can only be congruent with 0, 2, 3, or 6.
Here are the remainders for x=0 through 9:
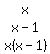
matrix%283%2C1%2Cx%2Cx-1%2Cx%28x-1%29%29matrix%283%2C5%2C0%2C1%2C2%2C3%2C4%2C8%2C0%2C1%2C2%2C3%2C0%2C0%2C2%2C6%2C3%29matrix%283%2C5%2C5%2C6%2C7%2C8%2C0%2C4%2C5%2C6%2C7%2C8%2C2%2C3%2C6%2C2%2C0%29
If you add those differences for the two digits, we should get 0 or 9.
The only choices are 0%2B0=0 and 3%2B6=9
0%2B0 can only be obtained for 10, 11, 19, 90, 91, 99, but all those numbers fail the first requirement we found based on divisibility by 2.

To make 3%2B6=9,
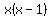x%28x-1%29 is congruent with 6 only for the odd digits 3 and 7, which can only be units digits.
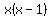x%28x-1%29 is congruent with 3 only for the even digits 4 and 6, which will have to be tens digits.
The only choices left are 43, 47, 63, and 67.
43%3C%3E4%5E2%2B3%5E2-18=16%2B9-18=7 so 43 is not a solution
63%3C%3E6%5E2%2B3%5E2-18=36%2B9-18=27 so 63 is not a solution
47=4%5E2%2B7%5E2-18=16%2B49-18=highlight%2847%29
67=6%5E2%2B7%5E2-18=36%2B49-18=highlight%2867%29

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

A two digit number is 18 less than the sum of the squares of its digits. How many such numbers are there?

Let tens and units digits be T and U, respectively
Then: 10T+%2B+U+=+T%5E2+%2B+U%5E2+-+18
T%5E2+-+10T+%2B+U%5E2+-+U+-+18+=+0

Since the number is 18 less than the sum of the squares of its digits, then its units digit is greater than its tens digit, or U > T.
Therefore, with 9 being the largest digit, we:

Let U = 9
T%5E2+-+10T+%2B+U%5E2+-+U+-+18+=+0
T%5E2+-+10T+%2B+81+-+9+-+18+=+0
T%5E2+-+10T+%2B+54+=+0 ----- T is NOT an INTEGER

Let U = 8
T%5E2+-+10T+%2B+U%5E2+-+U+-+18+=+0
T%5E2+-+10T+%2B+64+-+8+-+18+=+0
T%5E2+-+10T+%2B+40+=+0 ----- T is NOT an INTEGER

Let U = 7
T%5E2+-+10T+%2B+U%5E2+-+U+-+18+=+0
T%5E2+-+10T+%2B+49+-+7+-+18+=+0
T%5E2+-+10T+%2B+24+=+0
T, or tens digit = 6 or 4

This means that the number could be highlight_green%2867%29, or highlight_green%2847%29

Let U = 6
T%5E2+-+10T+%2B+U%5E2+-+U+%96+18+=+0
T%5E2+-+10T+%2B+36+-+6+-+18+=+0
T%5E2+-+10T+%2B+12+=+0 ----- T is NOT an INTEGER

No need to go any further since T ≠ U, and U > T

You can do the check!!

Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com. Further help is available, online or in-person, for a fee, obviously.

For FREE info and answers to questions about the ASVAB exam, the NYS 3 – 8 city/state wide exams, GENERAL MATH QUESTIONS, MATH HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra, Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE, GRE, CLEP, and the GED, you can visit: http://asvabstudyzone.freeforums.net/.