Question 79474: This problem I am having alot of trouble trying to figure out. Please Help!!
Mutt is half as old as Jeff will be when Mutt is twice as old as Jeff was when Mutt was half as old as Jeff is now. In five years, the sum of Mutt’s and Jeff’s ages will be 100. How old are Mutt and Jeff now?
Found 2 solutions by ankor@dixie-net.com, josmiceli:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Mutt is half as old as Jeff will be when Mutt is twice as old as Jeff was when Mutt was half as old as Jeff is now. In five years, the sum of Mutt’s and Jeff’s ages will be 100. How old are Mutt and Jeff now?
:
I think the 1st sentence just means "Mutt is half as old as Jeff"
:
M = .5J
:
The sentence "In five years, the sum of Mutt’s and Jeff’s ages will be 100.":
(M + 5) + (J + 5) = 100
M + J + 10 = 100
M + J = 100 -10
M + J = 90
Substitute .5J for M
.5J + J = 90
1.5J = 90
1.5J = 90/1.5
J = 60 years
Then:
M = 30 years old
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! Wow! this problem is either pretty tough or I'm just not reading it right.
Even if I'm off base, you might get something out of my method.
The thing to watch carefully is the words "now" and "when" and phrases
"will be" and "was".
Let M = Mutt's age now
Let J = Jeff's age now
The problem is saying that Mutt's age now is half of Jeff's age at
some future time. I'll call that time 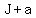 where a is in years where a is in years
So now I've got 
When Jeff is 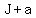 years old, Mutt will be years old, Mutt will be 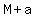 years old years old
The problem says that Mutt's age then will be twice what Jeffs
age was at some time in the past. I can now say 
where b are the years to be subtracted from M and J.
At this time in the past, -b years, what was Mutts age? The problem says
it was  , half as old as Jeff is now. , half as old as Jeff is now.
Going back,
 What's a in this equation? To find it, solve What's a in this equation? To find it, solve
 for a. for a.

substituting,


 What's b? Use What's b? Use  and solve for b. and solve for b.





Now use the last piece of information



 Jeff's age now Jeff's age now

 Mutt's age now Mutt's age now
I plugged the answers back into the equations and they checked,
but I've been wrong before, so use your judgement.
|
|
|