SOLUTION: suppose a population doubles every 20 years. Then by what percentage does it increase each year?

suppose a population doubles every 20 years. 
Then by what percentage does it increase 
each year?

This is the same problem and has the same 
answer as this one:

$1000 deposited in a savings account compounded 
annually grows to $2000 in 20 years.  What is 
the rate of interest?



with A = 2000, P = 1000, 
r unknown, n = 1 (compounded 1 time a yaer),
n = 20.



Divide both sides by 1000



Take the twentieth root of both sides









So the yearly rate is slightly over 3.5%. 

----------------------------------------------------------

Or, if your teacher doesn't like to pretend it's money, then 

Let x be the yearly percentage expressed as a decimal.
Suppose the population at the beginning of the first year is P.
Then:

At the end of the 1st year it is P + Px = P(1 + x)
At the end of the 2nd year it is P(1 + x) + xP(1 + x) = P(1 + x)2
At the end of the 3rd year it is P(1 + x)2 + xP(1 + x) = P(1 + x)3
...
...
...
At the end of the 20th year it is P(1 + x)20

Since it has doubled at the end of 20 years we set that equal to 2P

     P(1 + x)20 = 2P

Divide through by P

      (1 + x)20 = 2

Take thwentith roots of both sides
                    
         1 + x =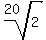  

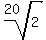             x =  - 1

             x = 1.035264924 - 1

             x = .035264924 or slightly over 3.5%
 
Edwin