|
Question 7939: I'm a Freshmen at Westside high School in Houston Tx and I am currently having problems with memory. My teacher is hard to understand by her acsent. I am having problems with solving equation w/distributing and combining like terms. Please fully teach me how to do this again. Thank you.
Answer by prince_abubu(198)   (Show Source): (Show Source):
You can put this solution on YOUR website! Distributive property:
a(b + c + d) = ab + ac + ad
Sometimes, they will put a term outside a parentheses. What the distributive property tells you is that you CAN, and at times, you'll have to multiply the term outside with EACH and EVERY term inside the parentheses. Here's a live example:
3(2x - 7y + 5b) = 6x - 21y + 15b
What we did was multiply the 3 to EVERY single term inside the parentheses.
WARNING. Many think that 3(2x - 7y + 5b) = 6x - 7y + 5b. That is WRONG. They did that thinking that you only have to multiply the 3 to the first term, and after that you'd run out of 3's. That's why it's called the distributive property! You distribute (multiply) to EVERY term inside the parentheses.
----------------------------------------------------------------------------
Like terms.
The concept of like terms is one that you MUST nail down before going on in Algebra. (The other one you need to nail down is addition and subtraction of integers, especially when you're dealing with negative numbers). What exactly are like terms?
First up, let's straighten out what we mean by "term". A term can be:
1. A single number. Example: 4, 2, -83
2. A single variable. Example: x, n, c
3. Two or more variables multiplied together. Example xy, mx, abc
4. A constant multiplied to a variable or variables. Example: 4x, 5xy, -18abc
5. As described by #2, #3, or #4, when one or more of the variables is/are raised to a power. Example: 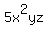 , , 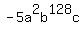 , , 
If they gave you two terms, how do you tell if they're like terms? They are like terms IF: (BTW, both listed MUST be true)
1. They have the same variable or variables.
2. The same variables MUST be raised to the same power.
For example, 2a and 5a are like terms because they have the same variable a, and in both terms, the a is raised to the same power (which is 1, but we don't write power 1, kind of like when you don't really say the word "you" before a command when you tell someone to do something).
Another example: 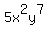 and and 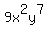 are like terms because they have the same variables, and the corresponding variables have the same powers! AKA, both x's are raised to the 2 and both y's are raised to the 7. are like terms because they have the same variables, and the corresponding variables have the same powers! AKA, both x's are raised to the 2 and both y's are raised to the 7.
----------------------------------
Then what are NOT like terms?
Un-example: 7 and 3x. The 7 does not have a variable, and the 3x does. That already breaks rule #1.
Un-example: 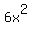 and and  . Same variable but different powers. Powers MUST be the same for each variable on both terms! . Same variable but different powers. Powers MUST be the same for each variable on both terms!
Un-example: 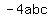 and and 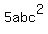 . Same variables but the c's don't match powers. . Same variables but the c's don't match powers.
Un-example: 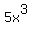 and and 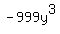 . Same powers but different variables. . Same powers but different variables.
-------------------------------------
So why know about like terms? Because knowing so ALLOWS you to know what you CAN vs. what you CAN'T combine when adding terms together. You may only add or subtract like terms. If both terms don't follow the two rules, you CAN'T add or subtract them.
Example: 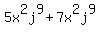 may be added to become may be added to become 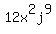 because the variables are the same AND each variable has the same power in both terms. because the variables are the same AND each variable has the same power in both terms.
Un-Example: 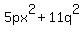 just has to be left that way because the variables don't match, although you see that variables are raised to the 2nd power in both terms. just has to be left that way because the variables don't match, although you see that variables are raised to the 2nd power in both terms.
|
|
|
| |