SOLUTION: Find all complex zeros of p(x)= x^4+2x^3+x^2+18, if x=1-isqrt(2) is a zero of p(x).

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Find all complex zeros of p(x)= x^4+2x^3+x^2+18, if x=1-isqrt(2) is a zero of p(x).      Log On


   

Question 793781: Find all complex zeros of p(x)= x^4+2x^3+x^2+18, if x=1-isqrt(2) is a zero of p(x).
Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!

x4+2x3+x2+18

We use synthetic division:

1-i√2|1    2      1       0       18
     |     1-i√2  1-4i√2 -6-6i√2 -18
      1    3-i√2  2-4i√2 -6-6i√2   0

So we have now factored the polynomial as

[x-(1-i√2)][x³+(3-i√2)x²+(2-4i√2)x+(-6-6i√2)]

Now we know that since 1-i√2 is a zero, so is
its conjugate 1+i√2, so we divide the third 
degree polynomial synthetically, this time by 1+i√2

1+i√2|1    3-i√2  2-4i√2 -6-6i√2
     |     1+i√2  4+4i√2  6+6i√2
      1    4      6       0

So now we have factored the polynomial as

[x-(1-i√2)][x-(1+i√2)](x²+4x+6)

Now we find the zeros of x²+4x+6 by the quadratic formula

x²+4x+6 = 0

x = %28-4+%2B-+sqrt%284%5E2-4%2A1%2A6+%29%29%2F%282%2A1%29+

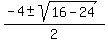x = %28-4+%2B-+sqrt%2816-24+%29%29%2F2

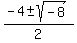x = %28-4+%2B-+sqrt%28-8%29%29%2F2

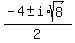x = %28-4+%2B-+i%2Asqrt%288%29%29%2F2

x = %28-4+%2B-+i%2Asqrt%284%2A2%29%29%2F2

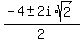x = %28-4+%2B-+2i%2Asqrt%282%29%29%2F2

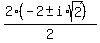x = %282%28-2+%2B-+i%2Asqrt%282%29%29%29%2F2

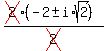x = %28cross%282%29%28-2+%2B-+i%2Asqrt%282%29%29%29%2Fcross%282%29

x = -2±i√2

So -2+i√2 and -2-i√2 are solutions.

Thus we have now factored the entire polynomial as

[x-(1-i√2)][x-(1+i√2)][x-(2-i√2)][x-(-2+i√2)]

and the four zeros are all imaginary.  They are:

1-i√2, 1+i√2, 2-i√2, -2+i√2

Edwin