Question 793364: are consecutive angles of a parallelogram called corresponding angles?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I may call them consecutive interior angles. They are supplementary, meaning that their measures add up to  . .
Usually we call corresponding angles the angles that "are the same" in one figure and another (usually triangles).

If the sides of triangles ABC and XYZ are congruent (the same length),
with AB=XY, BC=YZ, and CA=ZX, we say that the triangles are congruent,
and that sides AB and XY are corresponding sides.
The same is said about the pairs of sides BC and YZ, and CA and ZX.
The angles are also in pairs of corresponding angles (A with X, B with Y, C with Z), which are congruent (an important theorem in geometry).
The fact that the sides are congruent means the triangles are congruent (they are the same triangle maybe moved, and/or rotated, and/or flipped).
And the fact that triangles are congruent means that the corresponding angles are congruent, and you say that it is because of
CPCTC = Congruent Parts of Congruent Triangles are Congruent.
Another case where we talk about corresponding angles is when we have two parallel lines intersected by a third line that we call a transversal.
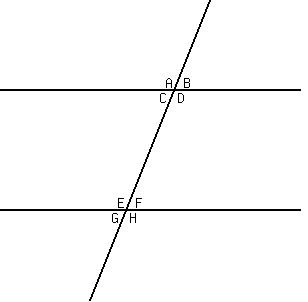 The pairs (A,E), (B,F), (C,G), and (Dd,H) are called corresponding, meaning that they are in the same position with respect to one parallel and the transversal. The pairs (A,E), (B,F), (C,G), and (Dd,H) are called corresponding, meaning that they are in the same position with respect to one parallel and the transversal.
Corresponding angles are congruent there too.
Other pairs of angles have special names too.
Pairs that are opposed at the vertex, like (A,D) are called vertical. They are congruent too.
Angles like A and H, outside the parallel lines and on alternate sides of the transversal, are called alternate exterior. They are congruent too.
Angles, like C and F, inside the parallel lines and on alternate sides of the transversal, are called alternate interior. They are congruent too.
Pairs of angles like C and E, inside the parallel lines and on the same side of the transversal are called consecutive interior angles. They are supplementary, meaning that their measures add up to  . .
|
|
|