Question 792243: P has degree 2 and zeros
1 + i
5
and
1 − i
5
.
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Recheck your problem description. If P is degree two, then you have TWO zeros; you cannot have zeros 1+i, 1-i, and 5 as the zeros. IF you have 1+i as a zero, then you ALSO have 1-i as a zero because complex zeros occur in P as "Conjugate Pairs", so you cannot also have 5 as a zero. If your zeros are supposed to be 1+i and 5, then you must also have 1-i; and this means P must be AT LEAST degree 3.
For degree THREE, your question would work and have a solution, but not for degree TWO.
You would, for degree THREE, have factors for P being 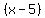 , , 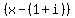 , and , and 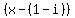 . .
Recheck your problem description from your book or source carefully, and then ask what you really want help with.
|
|
|