Question 792157: I need help on a ONE UNKNOWN(Very strict on that) word problem on coins. "If a purse contains 27 bills in 1 dollars and 5 dollars and its total value is 83 dollars, find the number of 1$ and 5$ in the purse
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE ALGEBRA WAY:
 = number of 5 dollar bills = number of 5 dollar bills
So, 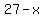 = number of 1 dollar bills = number of 1 dollar bills
 = value (in dollars) of all the 5 dollar bills = value (in dollars) of all the 5 dollar bills
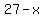 = value (in dollars) of all the 1 dollar bills = value (in dollars) of all the 1 dollar bills
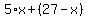 = value (in dollars) of all the bills in the purse = value (in dollars) of all the bills in the purse
The equation you need is

Simplifying and solving:






 is the number of 5 dollar bills in the purse is the number of 5 dollar bills in the purse
 is the number of 1 dollar bills in the purse is the number of 1 dollar bills in the purse
THE FIFTH GRADER WAY:
Maybe that purse belongs to a person that works the morning shift as a server at the local diner.
The server goes to work with an empty purse, and comes back home with money earned as tips.
By the end of the shift, that person has accumulated 83 dollars in tips, all in dollar bills.
Since that is too bulky to fit in the purse, the server goes to the cashier and exchanges five one dollar bills for one 5 dollar bill, ending with 4 less bills.
That makes the money less bulky, but it is still too bulky, so the server repeats the procedure again and again, until there are only 27 bills, and the money is not too bulky to fit in the purse.
It is a lot less bulky because now the total number of bills is 56 less than before.
83 - 27 = 56
Big difference!
How many times did the server exchange five one dollar bills for one 5 dollar bill, reducing the number of bills by 4 each time?
56 divided by 4 = 14.
Since each time the server got one 5 dollar bill in the exchange, there are noe 14 of those 5 dollar bills in the purse.
The rest of the bills in the purse are 1 dollar bills.
How many 1 dollar bills are in the purse.
27 - 14 = 13.
NOTE: It is good to be as smart as that fifth grader, but the story is shorter when told in algebra.
That fifth grader will be very good at algebra (unless someone tells him/her that algebra is supposed to be difficult, and that since the fifth grader does not know algebra, he/she should stop thinking by himself/herself and should just do as the teacher says).
|
|
|