Question 791452: An air puck of mass 0.23 kg is tied to a cord and allowed to revolve in a circle of radius 1.1 m on a frictionless table. The other end of the cord passes through a hole in the center of the table and is attached to a mass 1.1 kg. The suspended mass is in equilibrium while the puck on the table revolves. What is the speed of the puck in meters per second?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! In physics class problems cords have no mass, and there would be no friction of the cord at the hole either.
The centripetal acceleration of the air puck, 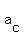 , in , in 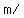 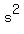 , is , is
 with with
 = linear velocity of the puck, and = linear velocity of the puck, and
 = radius of the trajectory of the puck = radius of the trajectory of the puck
The centripetal force, 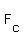 , that keeps the air puck in that steady circular motion is the mass of the puck times the centripetal acceleration: , that keeps the air puck in that steady circular motion is the mass of the puck times the centripetal acceleration:

That centripetal force is the weight of the 1.1kg mass suspended from the end of the cord, which is equal to that mass times the acceleration of gravity,   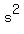 , so , so
  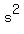
  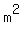  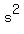
So,   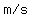
|
|
|