Question 791353: x[squared]-1=15
The answer is x[squared]=16
The final answer is x=4
My question: When you simplify x[squared]-1=15, by adding -1 to 15, why does the answer come out to x[squared]=16 and not x[squared]=-14? Isn't -1+15 equal to -14? If the original equation were x[squared]+1=15, then I could understand why the answer would be a positive 16. Aren't you supposed to take into consideration the minus sign in front of the 1 when adding it to 15?
Note: The original equation was cross multiplying fractions. It was x+1 over 3 = 5 over x-1. OR x+1/ 3=5/ x-1. Which then is simplifies to x[squared]-1=15.
Answer by fcabanski(1391)   (Show Source): (Show Source):
You can put this solution on YOUR website! You don't add -1 to 15. You add 1 to both sides. The goal is to isolate x, while maintaining balance. An equation is like a scale, or balance, with both sides the same. If you want to remove -1 from the left side, you have to add 1. -1 + 1 = 0. If you add 1 to the left, you have to add 1 to the right to maintain the balance.

Add one to both sides.

 Square root both sides. Square root both sides.
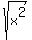 = + or - = + or - 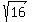
x = + or - 4.
-4 * -4 = 16 and 4 * 4 = 16. When you square root both sides, you have to remember it's + or - square root.
|
|
|