SOLUTION: 16 / (x+2) = 1 + 2/(x-4) I first eliminated the denominator x+2, then the denominator x-4. Simplifying and setting equal to 0, I get x = -6, -10. These solutions do not work,

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: 16 / (x+2) = 1 + 2/(x-4) I first eliminated the denominator x+2, then the denominator x-4. Simplifying and setting equal to 0, I get x = -6, -10. These solutions do not work,       Log On


   

Question 790553: 16 / (x+2) = 1 + 2/(x-4)
I first eliminated the denominator x+2, then the denominator x-4. Simplifying and setting equal to 0, I get x = -6, -10. These solutions do not work, but their positives do. I don't understand how to solve this equation without getting negative values for x.
Thanks in advance.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I get 6 and 10.
You must have made some small mistake.
It is very hard to notice one's own mistakes.
16+%2F+%28x%2B2%29+=+1+%2B+2%2F%28x-4%29
Multiplying both sides times 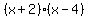%28x%2B2%29%28x-4%29 I get

which simplifies to
16%28x-4%29+=+%28x%2B2%29%28x-4%29+%2B+2%28x%2B2%29
16x-64+=+x%5E2-2x-8+%2B+2x%2B4
16x-64+=+x%5E2+-8+%2B4
16x-64+=+x%5E2-4
0+=+x%5E2-4-16x%2B64
x%5E2-16x%2B60=0
Factoring, I get
%28x-6%29%28x-10%29=0
So, either x-6=0 --> highlight%28x=6%29,
or x-10=0 --> highlight%28x=10%29.

If you do not like factoring, you could use the quadratic formula, or "complete the square" instead.

Completing the square:
x%5E2-16x%2B60=0
x%5E2-16x=-60
x%5E2-16x%2B64=-60%2B64
%28x-8%29%5E2=4
So either x-8=2 --> x=2%2B8 --> highlight%28x=10%29,
or x-8=-2 --> x=-2%2B8 --> highlight%28x=6%29

Using the quadratic formula:
The solutions to ax%5E2%2Bbx%2Bc=0 are given by x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+.
In the case of x%5E2-16x%2B60=0,
a=1, b=-16, and c=60, so
.
The solutions are
x=%2816+%2B+4%29%2F2=20%2F2=highlight%28x=10%29
and x=%2816+-+4%29%2F2=12%2F2=highlight%28x=6%29