SOLUTION: How do I find the exact values of all the angles between 0 rad and 2pi rad for which cos(x)=-square root 3 / 2?

Algebra ->  Trigonometry-basics -> SOLUTION: How do I find the exact values of all the angles between 0 rad and 2pi rad for which cos(x)=-square root 3 / 2?      Log On


   

Question 790215: How do I find the exact values of all the angles between 0 rad and 2pi rad for which cos(x)=-square root 3 / 2?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The graph of cos%28x%29 looks like this:
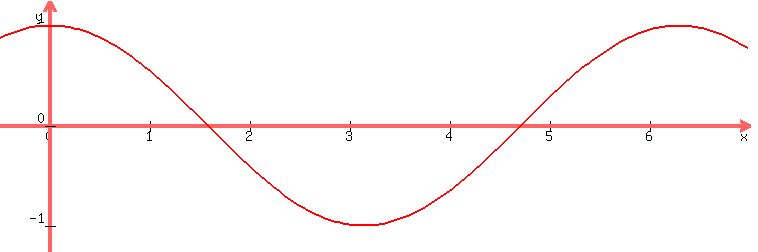
graph%28750%2C250%2C-0.5%2C7%2C-1.25%2C1.25%2Ccos%28x%29%29
Sine and cosine range from -1 to 1, and have a period of 2pi (4 quadrants).
Over a period, they go full circle, up to 1, down to -1, and back.
So, within a period, they go twice through any value other than the extremes, -1 and 1, once on the way up, and another time on the way down, and in different quadrants.
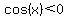cos%28x%29%3C0 in quadrants II (pi%2F2%3Cx%3C=pi), and III (pi%3C=x%3C3pi%2F2, so there will be a solution for cos%28x%29=-sqrt%283%29%2F2 in each of those quadrants.
cos%28pi%2F6%29=sqrt%283%29%2F2 is one of 5 numbers that you will see in many problems about trigonometric function values.
-sqrt%283%29%2F2 is the opposite value, corresponding to the supplementary angle, pi-pi%2F6=highlight%285pi%2F6%29 and to pi%2Bpi%2F6=highlight%287pi%2F6%29.
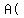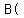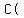Points %22A+%28%22sqrt%283%29%2F2%22%2C%221%2F2%22%29%22, %22B+%28%22-sqrt%283%29%2F2%22%2C%221%2F2%22%29%22, and %22C+%28%22-sqrt%283%29%2F2%22%2C%22-1%2F2%22%29%22 are circled
cos%28pi-pi%2F6%29=cos%285pi%2F6%29=-sqrt%283%29%2F2
cos%28pi%2Bpi%2F6%29=cos%287pi%2F6%29=-sqrt%283%29%2F2

EXTRA:
The 5 trigonometric function values that you will often see:
cos%280%29=highlight%281%29=sin%28pi%2F2%29
cos%28pi%2F6%29=highlight%28sqrt%283%29%2F2%29=sin%28pi%2F3%29
cos%28pi%2F4%29=highlight%28sqrt%282%29%2F2%29=sin%28pi%2F4%29
cos%28pi%2F3%29=highlight%281%2F2%29=sin%28pi%2F6%29
cos%28pi%2F2%29=highlight%280%29=sin%280%29