Question 789606: Pat and Kim are talking on the telephone during a thunderstorm. After one of the lighting flashes, Pat hears the rumble of thunder twice-the first sound coming through the open window, and the second sound coming through the telephone ten seconds later. Given that Pat lives two miles east of the center of town, Kim lives two miles west of the center of tow, both on the same east-west road, and that sound takes five seconds to travel through the air, draw a map that shows some of the places where the lightning could have struck. for example, could the lightning have struck the road on which Pat and Kim live? Assume that light and electricity take no time to reach their destinations.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Maybe one or two words are missing.
It should say "sound takes five seconds to travel 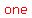 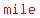 through the air." through the air."
Since 1 mile is about 1609 meters, and the speed of sound at sea level is often quoted as 340 m/s (it depends a bit on temperature, air humidity, and altitude), sound would take about
 to travel one mile through the air. to travel one mile through the air.
If sound takes 5 seconds to travel 1 mile, and Pat heard the thunder through the open window first, and through the phone 10 seconds later, Pat lives 2 miles closer than Kim to the place where lightning struck.

Where do we find places that are 2 miles closer to Pat than to Kim?
The most obvious place would be on the east-west road where Kim and Pat live, 1 mile east of the center of town.
That is 1 mile from Pat and 3 miles from Kim, and  . .
There are many other places that are 2 miles closer to Pat than to Kim.
You could find two places that are 2 miles from Pat and 4 miles from Kim. One is north of the east-west road, and the other one is south of it, and they are symmetrical with respect to that road.
You could find two places that are 3 miles from Pat and 5 miles from Kim, also symmetrical with respect to the east-west road.
One such place is 3 miles north of Pat's house. That places, Pat's house, and Kim's house form a right-angled triangle, with the right angle at Pat's house.
Here's my map, with some lightning strike sites marked with red circles:

The answer expected from you depends on the level of the math class you are taking in school.
The expected answer could be to draw a map, using a ruler and a compass.
With the ruler you would draw the east-west road where Kim and Pat live, and mark, the center of town, and places 1 mile intervals to either side, labeling the points that are Kim's and Pat's houses.
Marking the spot on the east-west road at 3 miles from Kim's and 1 mile from Pat's (1 mile east of town center) is no problem.
For the other spots, you would use the compass to locate places that are at the needed distances from kim's and Pat's houses.
You could set the span of the compass to a distance of 4 miles (the distance from Kim's to Pat's, and make arcs centered on Kim's house on both sides of the east-west road near Pat's house. Those arcs would mark places that are 4 miles from Kim's house. Then, adjusting the compass to a span of 2 miles (the distance from either house to the center of town), you could make arcs centered at Pat's house. Those arcs would mark places 2 miles from Pat's house. The points where the new arcs intersect the previous arcs. would be 4 miles from Kim's house and 2 miles from Pat's.
Then you could pick another pair of distances, such as 5, and 3, and mark the 2 spots that are 5 miles from Kim's and 3 miles from Pat's.
In my map
From the wording of your problem, I do not think that you are taking pre-calculus or calculus.
If you were taking pre-calculus, or calculus, you could be expected to say that " the locus of the places where lightning could have struck is one arm of a hyperbola with Pat's and Kim's houses as foci".
Maybe you would even sketch the hyperbola and write the equation for it.
|
|
|