Question 789334: Ms Ho Numbered 30 pupils by writing 1,2,3.....28,29,30 on their name tags . She arranged all the 30 pupils to stand in a row, starting from number 1 to number 30.
Next, for every second pupil, she asked each pupil to sit.
Then, for every third pupil, she asked each standing pupil to sit and each sitting pupil to stand.
She followed the same pattern (which is to ask each standing pupil to sit amd each sitting pupil to stand) for every fourth, every fifth pupil, so on till the 30th pupil.
How many pupils were standing after the whole process was completed?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  pupils will be left standing. pupils will be left standing.
Student number 1 stands the whole time.
The other students will have to change positions (between standing and sitting) at least once, but most of them change positions an odd number of times and end up sitting.
Only the pupils with numbers 9, and 16, are told to change positions an
even number of times and end up standing.
THE EXPLANATION:
When Ms Ho asks that every second student sits, she is making all the students whose numbers are multiples of 2 change positions from standing to sitiing.
When Ms Ho asks that every third student change position, she is asking all the students whose number is a multiple of 3 to change positions.
The pupils change positions when one of the factors of their number is called, and most will end up sitting at some point.
Students with a prime number have it easy. The only factors of their number are 1 and the prime number itself, and 1 does not count, so they just sit once, when their number is called.
Student number 29 stands for a long time, and finally sits when Ms Ho says that every 29th student has to change positions.
Student number 24 gets quite a workout, because 24 has 2, 3, 4, 6, 8, 12, and 24 for factors. That student sits when every second pupil has to sit; stands when every third student has to change positions; sits again when every fourth pupil has to change positions; stands for being one of every 6th student; sits for being one of every 8th student; stands again for beig one of every 12th student, and finally sits when every 24th student has to move.
The number of factors of a number depends on their prime factorization.
For 24, the prime factorization is

The possible factors of 24 are all the combination products of the form 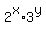 . .
 , ,
 , ,
 , ,
 , ,
 , ,
 , and so on, up to , and so on, up to 
The factors are the products of powers of 2, and 3, because 2, and 3 are the prime factors of 24.
The exponents x, and y are integers between 0 and the exponent in the prime factorization, so  and and  . .
That gives us 4 choices for x (0, 1, 2, and 3), and 2 choices (0, and 1) for y, for a total of  factors of 24, including 1, and 24 itself. factors of 24, including 1, and 24 itself.
The number of factors will be even for any number that has a 1 or a 3 for an exponent in the prime factorization,
That is what happens for 12, because the prime factorization  has a 1 for one of the exponents. has a 1 for one of the exponents.
The same happens for  because of that number 3 as an exponent. because of that number 3 as an exponent.
The only numbers between 1 and 30 with an odd number of factors are
 with factors 1, 3, and 9. with factors 1, 3, and 9.
and  with the 5 factors 1, 2, 4, 8, and 16. with the 5 factors 1, 2, 4, 8, and 16.
The pupils with numbers 9, and 16, are told to change positions an
even number of times, because they have to do so each time one of their factors other than 1 is called, and 9 and 16 have an even number of factors other than 1.
So pupils number 9 and 16 end up standing.
|
|
|