SOLUTION: I sent this problem and received an answer, thank you but it is not the answer given on my work, which I got wrong. The question was. A stoplight is red 20% of the time. If som

Algebra ->  Probability-and-statistics -> SOLUTION: I sent this problem and received an answer, thank you but it is not the answer given on my work, which I got wrong. The question was. A stoplight is red 20% of the time. If som      Log On


   

Question 789033: I sent this problem and received an answer, thank you but it is not the answer given on my work, which I got wrong. The question was.
A stoplight is red 20% of the time. If someone drives through this light 10 times a week, what is the probability they will stop at 3 times. The answer was .322 and I can't figure out how to get this answer.
Please help
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
You are missing one crucial word in the wording of your problem. Maybe it's a typo in the problem as given to you, or maybe you inadvertently skipped that word when reading or transcribing the problem. SInce I do not know what explanation you got before, I will give you a lengthy (but hopefully very clear) full explanation.

If someone drives through that intersection once the probability of stopping would be 0.2 and the probability of not having to stop is 0.8.
With s= having to stop and g= going through without needing to stop, the whole situation can be described as
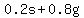
0.2s%2B0.8g

If a person has to drive through that intersection twice, the situation is

meaning that there is
0.04 (4%) probability that they will have to stop both times,
0.64 (64%) probability that the will be able to drive through without stopping both times, and
0.32 (32%) probability that they will stop one of the two times (0.16 or 16% chance that they will have to stop only the first time, and 0.16 or 16% chance that they will have to stop only the second time).
The sum is 1, which is the probability of getting through the intersection twice one way of another, if you go through the intersection twice.

If the person has to drive through that intersection 10 times, the situation is
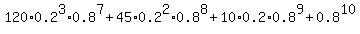
%22%2B+...+%2B%22120%2A0.2%5E3%2A0.8%5E7%2B45%2A0.2%5E2%2A0.8%5E8%2B10%2A0.2%2A0.8%5E9%2B0.8%5E10
The 11-term sum is 1, which is the probability of getting through the intersection one way of another 10 times, if you go through the intersection 10 times.
Each term represents the probability of having to stop a certain number of times.
0.2%5E10=1.024%2A10%5E%28-7%29 or 0.00001024% is the probability of having to stop all 10 times.
10%2A0.2%5E9%2A0.8=4.096%2A10%5E%28-7%29 or 0.00004.096% is the probability of having to stop exactly 9 out of the 10 times.
45%2A0.2%5E8%2A0.8%5E2=7.3728%2A10%5E%28-5%29 or 0.0073728% is the probability of having to stop exactly 8 out of the 10 times.
120%2A0.2%5E7%2A0.8%5E3=0.000786432 or 0.0786432% is the probability of having to stop exactly 7 out of the 10 times.
On the other side of the sum,
120%2A0.2%5E3%2A0.8%5E7=0.201326592 or 20.1326592% is the probability of having to stop exactly 3 out of the 10 times.
(67.77799526%) is the probability of having to stop either exactly 2, or 1, or 0 times.
The opposite situation, having to stop more than 2 times (at least 3 times) is 1-0.677799526=0.322200474

That means having to stop maybe 3 times, maybe 4 times, maybe 5 times, maybe more times, maybe even 10 out of the 10 times, and that must have been the wording of the question if the answer was 0.322... The question should have been what is the probability they will stop "at least" 3 times?