SOLUTION: i need help on this word problem. One side of a rectangle is 4 in. longer than the other. If the sides are each increases by 2 in., the area of the new rectangle is 60 in^2. How lo

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: i need help on this word problem. One side of a rectangle is 4 in. longer than the other. If the sides are each increases by 2 in., the area of the new rectangle is 60 in^2. How lo      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 788911: i need help on this word problem. One side of a rectangle is 4 in. longer than the other. If the sides are each increases by 2 in., the area of the new rectangle is 60 in^2. How long are the sides of the original rectangle?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
THE FIFT GRADER APPROACH:
If the length and the width of the rectangle are each increases by 2 in., in the larger final rectangle the length will still be 4 in. longer than the width.
So we are looking for two numbers (measurements in inches) that multiply to yield 60 (square inches) for the area of the rectangle.
6%2A10=60, so the larger final rectangle is 6 inches wide by 10 inches long.
Then, the original smaller rectangle (before increasing each side by 2 inches) measured 6in-2in=highlight%284in%29 by 10in-2in=highlight%288in%29.

MAKING IT LOOK MORE DIFFICULT WITH ALGEBRA:
x= width of the original rectangle (in inches)
x%2B4= length of the original rectangle (in inches)
As we increase each side by 2 inches, we get
x%2B2= width of the new, larger rectangle (in inches)
x%2B4%2B2=x%2B6= length of the new, larger rectangle (in inches)
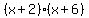%28x%2B2%29%28x%2B6%29= area of the new, larger rectangle (in square inches)
So, %28x%2B2%29%28x%2B6%29=60 is our equation.
Simplifying:
%28x%2B2%29%28x%2B6%29=60
x%5E2%2B6x%2B2x%2B12=60
x%5E2%2B8x%2B12=60
x%5E2%2B8x%2B12-60=0
x%5E2%2B8x-48=0
Now we need to solve that quadratic equation and I can see 3 options.

Solving by factoring:
x%5E2%2B8x-48=0
%28x%2B12%29%28x-4%29=0
The solutions to that equation are
x=-12 (from(x%2B12=0) and
and x=4 (from(x-4=0).
We discardthe solution x=-12 because the lwidth of a recatngle (in inches) must be a positive number.
x=highlight%284%29 is the width of the original rectangle (in inches)
x%2B4=4%2B4=highlight%288%29 is the length of the original rectangle (in inches).

Completing the square:
x%5E2%2B8x-48=0
x%5E2%2B8x=48
x%5E2%2B8x%2B16=48%2B16
%28x%2B4%29%5E2=64
x%2B4=highlight%288%29 is the length of the original rectangle in inches.
So, x=8-4=highlight%284%29 is the width of the original rectangle in inches.

Using the quadratic formula:
The solutions to an equation of the form ax%5E2%2Bbx%2Bc=0 can be calculated as
x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+
In the case of x%5E2%2B8x-48=0,
a=1, b=8, and c=-48, so

One solution to that equation is
x+=+%28-8+-+16%29%2F2+=-24%2F2=-12,
but that negative number cannot be the width of the original rectangle in inches.
The other solution is
x+=+%28-8+%2B+16%29%2F2+=8%2F2=highlight%284%29 and that is the width of the original rectangle in inches.
Then, x=4=4%2B4=highlight%288%29 is the length of the original rectangle in inches.