SOLUTION: SOS. I am not good at word problems. You have 10 fewer quarters than dimes and 5 fewer nickels than quarters. The total value of the coins is $4.75. How many quarters nickels and d

Algebra ->  Coordinate Systems and Linear Equations  -> Linear Equations and Systems Word Problems -> SOLUTION: SOS. I am not good at word problems. You have 10 fewer quarters than dimes and 5 fewer nickels than quarters. The total value of the coins is $4.75. How many quarters nickels and d      Log On


   

Question 786864: SOS. I am not good at word problems. You have 10 fewer quarters than dimes and 5 fewer nickels than quarters. The total value of the coins is $4.75. How many quarters nickels and dimes do you have?
Found 2 solutions by josgarithmetic, Edwin McCravy:
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
ASSIGN Variables to all quantities. Your exercise problem mentions and describes some different coins. There are quartes, dimes, and nickels; the amount of money is $4.75.

A way to pick the variables can be:
q = how many quarters
d = how many dimes
n = how many nickesl
All are variables, so far all unknown.

TRANSLATE THE DESCRIPTIONS INTO NUMERIC EXPRESSIONS OR EQUATIONS
"ten fewer quarters than dimes", d-10=q.
Think about that to see if it makes sense. Dimes... ten fewer.
"five fewer nickels than quarters", q-5=n.
Think carefully about this.
-------------------------If good so far, then continue--------------
The total money $4.75 is based on the count and value of the coins present.
q+d+n=4.75

Recheck the equations and neaten the system:
highlight%28q%2Bd%2Bn=4.75%29
highlight%28q=d-10%29
highlight%28n=q-5%29

Your next choice is, how do you want to solve the system? This is three equations in three unknowns.

Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
The other tutor used three unknowns.  Here is the way to do it 
with only one unknown.

SOS. I am not good at word problems. You have 10 fewer quarters than dimes and 5 fewer nickels than quarters. The total value of the coins is $4.75. How many quarters nickels and dimes do you have?
>>...10 fewer quarters than dimes...<<
We know from reading that, that there are more dimes and less quarters, and
that their numbers differ by 10.

So we can say that either of two ways: 
"smaller = larger minus 10", or
"larger = smaller plus 10".

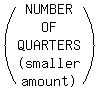
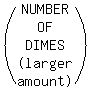%22%22=%22%22 MINUS 10     OR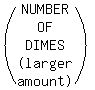  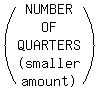   %22%22=%22%22 PLUS 10

>>...5 fewer nickels than quarters...<<
We know from reading that, that there are more quarters and less nickels, and
that their numbers differ by 5.

So we can also say that either of two ways:

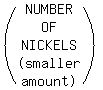
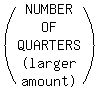%22%22=%22%22 MINUS 5     OR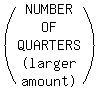  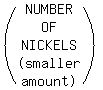   %22%22=%22%22 PLUS 5

Since QUARTERS appear in both sentences, we want to let the number of 
quarters be equal to the unknown, say q.

So we choose the two which have quarters on the right side:

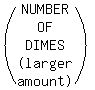
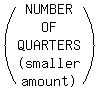%22%22=%22%22 PLUS 10    AND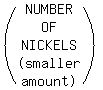  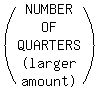   %22%22=%22%22 MINUS 5    

Number of dimes = q+10       AND     Number of q-5

So we have q quarters, q+10 dimes and q-5 nickels

>>...The total value of the coins is $4.75...<<
Now we turn those 3 numbers of coins all into a money equation.

q quarters are worth  $0.25(q)
q+10 dimes are worth  $0.10(q+10)
q-5 nickels are worth $0.05(q-5)

So we add those together on the left side and set it equal to $4.75:

$0.25(q) + $0.10(q+10) + $0.05(q-5) = $4.75

Drop the dollar marks and move the decimals two places right:

            25q + 10(q+10) + 5(q-5) = 475

Solve that for q, and that will be the number of quarters.
Then substitute for q to find how many dimes q+10 is and 
how many nickels q-5 is. 

Edwin