Question 785545: At what time after 8:00 PM
will the second hand bisect the
angle formed by the minute
hand and hour hand?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The hour hand sweeps through  in 12 hours ( in 12 hours ( ) )
That angular velocity could be stated as
 per minute. per minute.
The minute hand sweeps through  in 60 minutes in 60 minutes
That angular velocity could be stated as
 per minute. per minute.
The second hand sweeps through  in 1 minutes in 1 minutes
That angular velocity could be stated as
 per minute. per minute.
At 8:00:00 PM, the second hand amd the minute hand are pointing up, to 12, while the hour hand points to 8. They are forming 2 angles that add up to  : :
One is the 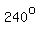 angle containing the numbers from 1 through 7, and the other is the angle containing the numbers from 1 through 7, and the other is the  angle containing the numbers 9, 10, ans 11. angle containing the numbers 9, 10, ans 11.
After 8:00:00 PM, the second hand starts racing towards the hour hand, ahead of the slower minute hand.
In 20 seconds it is 8:00:20 PM.
The second hand has swept  and is pointing at 4; the minute hand has swept only and is pointing at 4; the minute hand has swept only 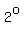 , and the hour hand has barely moved half a hair. , and the hour hand has barely moved half a hair.
At that point the second hand is almost bisecting the angle (about 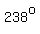 ) formed by the minute ) formed by the minute
hand and hour hand.
If we do not need to be too accurate, we could say that at that time it is bisecting the angle formed by the minute
hand and hour hand.
If we need to be more precise, we can calculate angles a s a funtion of time.
With  = minutes since 8:00:00 PM, the angles, counted clockwise betweeen the 12 o'clock position and each hand are: = minutes since 8:00:00 PM, the angles, counted clockwise betweeen the 12 o'clock position and each hand are:
 for the second hand, for the second hand,
 for the minute hand, and for the minute hand, and
 for the hour hand. for the hour hand.
To bisect bisecting the angle formed by the minute hand and hour hand, the second hand needs to form an angle of
 . .
(That is the average of 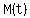 and and 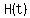 ). ).
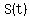 will be exactly that angle when will be exactly that angle when
 --> --> --> --> --> --> . .
That is the time in minutes after 8:00:00PM.
In seconds, it is  . .
The second hand first bisects the angle formed by the minute hand and hour hand at 8:00:20.18 PM.
It will happen again at about 8:00:50 PM, and again a little after 8:01:20 PM, and it will keep happening at intervals a hair longer than 30 seconds.
|
|
|