Question 78546: 2) Use the geometric sequence of numbers 1, 3, 9, 27, … to find the following:
a) What is r, the ratio between 2 consecutive terms?
Answer:
Show work in this space.
b) Using the formula for the nth term of a geometric sequence, what is the 10th term?
Answer:
Show work in this space.
c) Using the formula for the sum of a geometric sequence, what is the sum of the first 10 terms?
Answer:
Show work in this space.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! a)
The ratio r is the factor needed to go from term to term. To find the factor, divide any term by its previous term. So I chose 3 as the first term to be divided by 1
Ratio r:  pick any nth term and any previous term, such as the 2nd and 1st term. pick any nth term and any previous term, such as the 2nd and 1st term.
 I can also do it with 27 and 9 and it will still give me the same value I can also do it with 27 and 9 and it will still give me the same value

So r=3
b) Since we are multiplying by r each term, our sequence is simply

So to find the nth term ( ), we simply multiply the previous term ( ), we simply multiply the previous term (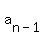 ) by r. ) by r.
So if we start at 1, to get to 3 we multiply 1 by r=3

Now to go from 3 to 9 we multiply by r again

Now to go from 9 to 27 we multiply by r again

Notice that for the 1st term 3 we have only 1 r, 2nd term we have 2 r's, etc. So the term we have determines the number of r's. In other words, the nth term is

So our sequence is 
Now let n=9 to find the 10th term (we started at n=0)

So the 10th term is 19,683
c) The sum of the first ten terms can be found by using

So let r=3



So the sum of the first ten terms are 29,524
|
|
|