Question 785437: An open rectangular tank is made from a steel plate of area 1440msquared. Its length is twice its width. If the dept of the tank is 4m lesth than the width, find the length of the tank.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = width in meters = width in meters
 = length in meters = length in meters
 = depth in meters = depth in meters
Obviously, the entire 1440m^2 of the steel plate will be used, without wasting any, or stetching/deforming the material.
That is probably far from realistic, but this is just a math problem.
We cannot expect to work on the design, because we have not given enough information. The design is someone else's problem.
The total surface of the tank includes the bottom, 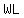 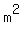 , ,
and the sides,  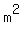 . .
Our equation is

Since L and W came expressed in terms of W, we can substitute those expressions to get an equation in terms of W only:






Dividing both sides of the equal sign by 8, we get

Factoring, we get
 with solutions with solutions  and and 
We throw away  because the width in meters cannot be a negative number. because the width in meters cannot be a negative number.
 --> --> 
The length of the tank is 
|
|
|