|
Question 785389: I am trying to solve a linear equation with three variables and I am stuck on this problem. My teacher said the answer is not in a fraction but is a whole number but every time I have tried to solve it I get a fraction.
3x-2y+3z=11
5x+2y-2z=4
-x+y+z=-7
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! When my solution does not check, or looks too complicated, I throw away my prior attempt, take a few deep breaths, and start again from scratch writing as big and neatly as possible on a large, clean piece of paper. I did that with your problem, twice, and the third time was a charm. (If I reviewed what I had done looking for the mistake, I would be most likely to miss it).
In  ,
-x+y+z=-7 looks like the simplest of the three equations.
I am going to use it to eliminate  from the other two.
(The sooner I eliminate the less likely I am to confuse it with a  ).
I multiply -x+y+z=-7 times 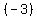 and add it to 3x-2y+3z=11:
3x -2y +3z = 11
3x -3y -3z = 21
______________
6x -5y = 32
I multiply -x+y+z=-7 times and add it to 5x+2y-2z=4:
5x +2y -2z = 4
-2x +2y +2z = -14
______________
3x +4y = -10
Now I have the equivalent system
I am going to combine 6x-5y=32 and 3x+4y=-10 to get an equation without  .
I multiply 3x+4y=-10 times 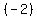 and add it to 6x-5y=32:
6x -5y = 32
-6x -8y = 20
___________
-13y = 52 ---------> y = 52 / (-13) -----> 
Now I have the equivalent system
Substituting y=-4 into 3x+4y=-10, I get
3x+4(-4)=-10 ------> 3x-16 = -10 ------> 3x=-10+16 ----> 3x=6 ---> x=6/3 ---> 
Now I have the equivalent system
Substituting x=2 and y= -4 into -x+y+z=-7, I get
-2 + (-4) +z = -7 ---> -2-4 +z = -7 ---> -6 + z = -7 --> z=-7+6 ---> 
|
|
|
| |
