SOLUTION: Given the equations, rewrite each as a quadratic equations in u, where u = e^x. Solve for u first then for x 1) e^2x - e^x =6 2)e^-2x - 3e^-x = -2

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: Given the equations, rewrite each as a quadratic equations in u, where u = e^x. Solve for u first then for x 1) e^2x - e^x =6 2)e^-2x - 3e^-x = -2      Log On


   

Question 785014: Given the equations, rewrite each as a quadratic equations in u, where u = e^x.
Solve for u first then for x
1) e^2x - e^x =6
2)e^-2x - 3e^-x = -2
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
If u = e%5Ex then u%5E2+=+e%5E%282x%29 - when multiplying a base to a power by the same base to a different power, add the powers. e%5Ex+%2A+e%5Ex+=+e%5E%28x%2Bx%29+=+e%5E%282x%29


e%5E2x+-+e%5Ex+=6+ means u%5E2+-u=6


u%5E2+-+u+-+6+=+0


(u-3)(u+2) = 0


u = 3 and u = -2


e%5Ex+=+3 Use the inverse function of e which is ln.


ln%28e%5Ex%29+=+ln%283%29


x = ln(3) = approximately 1.0986


For u=-2, do the same. e%5Ex+=+-2


ln%28e%5Ex%29+=+ln%28-2%29


x = ln(-2): ln of a negative number is not a real number. So discard this answer. If you want to find the imaginary number solution, it's 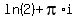ln%282%29+%2B+pi%2Ai = approximately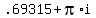 .69315+%2B+pi%2Ai


e%5E%28-2x%29+-+3e%5E%28-x%29+=+-2 is 1%2Fu%5E2+-3%2Fu+=+-2


Multiply all terms by u%5E2 to get 1+-+3u+=+-2u%5E2


2u%5E2+-3u+%2B+1+=+0


(2u-1)(u-1) = 0


2u = 1 so u = 1/2 so e%5Ex+=+1%2F2 and thus x = ln(1/2) = approximately -.693


u=1 so e%5Ex+=+1 so x = ln(1) = 0