SOLUTION: What is the Indian to factor a trinomial? I need an example. Someone at work mentioned to me and I am trying to figure it out

We have a lesson  on that here on algebra.com:

http://www.algebra.com/algebra/homework/quadratic/THEO-2011-08-28-02.lesson

The object is to get the discriminant b²-4ac on the right side

ax² + bx + c = 0

Get the constant term off the left side

ax² + bx     = -c

First we make the right side -c into -4ac, the second term of
the discriminant by multiplying through every term by 4a

4a²x² + 4abx     = -4ac

Now we add b² to both sides to finish getting the discriminant
on the right side.

4a²x² + 4abx + b² = b²-4ac

The left side factors as a perfect square

     (2ax+b)² = b²-4ac

Then we use the principle of square roots:

        2ax+b = ±√b²-4ac

Then solve for x

          2ax = -b±√b²-4ac

Then finally:

            x =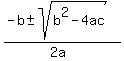 

Which is what you'd get if you used the quadratic formula.

Edwin