Question 784570: how do you solve for x algebraically for : 2sin^2x+5sinx=3
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
If you make a change of variable, it gets easier to write and easier to see the solution.
Substititing  , the equation turns into , the equation turns into

You probably know what to do with that equation.
I would do this:
 --> -->  --> --> 
From that last, factored equation, we get two solutions in terms of  : :
 --> -->  --> -->  and and
 --> --> 
In terms of  , ,  makes no sense. makes no sense.
On the other hand, from the other  value we get many values for value we get many values for 

To begin with, if we just stick to the first turn, with  , we have 2 solutions: , we have 2 solutions:  and and  , because , because
 and and 
If using radians rather than degrees, for  , the soluttions are , the soluttions are  and and  , because , because
 and and 
If you are not restricted to the first turn, there are infinite solutions, because co-terminal angles have the same trigonometric function values, so that all the solutions could be written as
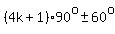 or or  for any integer for any integer  . .
(Making  gives you the solutions in the first turn). gives you the solutions in the first turn).
|
|
|